Trên hệ trục tọa độ xOy: cho tam giác ABC có A(-1;1), B(1;3) và trọng tâm G\(\left(-2;\dfrac{2}{3}\right)\). Tìm tọa độ M trên tia Oy sao cho tam giác MBC vuông tại M
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


gọi H(x;y) là chân đường cao hạ từ A
\(\overrightarrow{AH}\left(x-4;y-3\right)\);\(\overrightarrow{BC}\left(-5;-15\right)\)
có AH vuông góc với bc \(\Rightarrow\overrightarrow{AH.}\overrightarrow{BC}=\overrightarrow{0}\)suy ra được 1 phương trình
có B,H,C thẳng hàng suy ra \(\overrightarrow{BH}=k.\overrightarrow{BC}=\left(-5k;-15k\right)\Rightarrow x-2=-5k;y-7=-15k\Rightarrow\left(x-2\right):\left(y-7\right)=1:3\)có 2 phương trình 2 ẩn giải tìm được x;y

Biểu diễn ba điểm A, B, C trên hệ trục tọa độ Oxy ta được
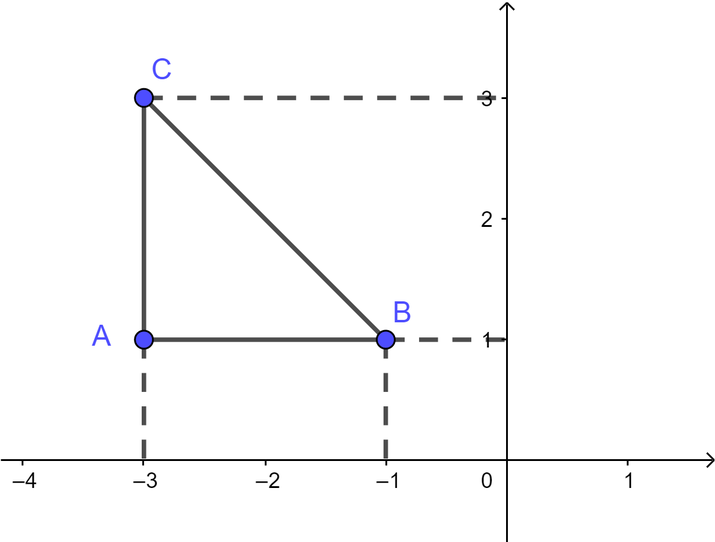
Quan sát hình vẽ ta thấy tam giác ABC là tam giác vuông tại A
Chọn đáp án C

Chọn B.
*) AH là đường cao của tam giác ABC.
*) Lập phương trình cạnh BC
B(1;-1), C(5;2) 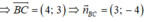
(BC): 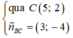
⇒ 3.(x - 5) - 4.(y - 2) = 0 ⇔ 3x - 15 - 4y + 8 = 0 ⇔ 3x - 4y - 7 = 0
Ta có:
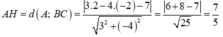
\(\left\{{}\begin{matrix}x_C=3x_G-x_A-x_B=-6\\y_C=3y_G-y_A-y_B=-2\end{matrix}\right.\) \(\Rightarrow C\left(-6;-2\right)\)
Gọi \(M\left(0;m\right)\) \(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{BM}=\left(-1;m-3\right)\\\overrightarrow{CM}=\left(6;m+2\right)\end{matrix}\right.\)
\(\overrightarrow{BM}.\overrightarrow{CM}=0\Leftrightarrow-6+\left(m-3\right)\left(m+2\right)=0\)
\(\Leftrightarrow m^2-m-12=0\Rightarrow\left[{}\begin{matrix}m=-3\\m=4\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}M\left(0;-3\right)\\M\left(0;4\right)\end{matrix}\right.\)