\(\text{Nối M với C}\)

\(\text{Xét :}\)\(\Delta MCH\perp H\text{ có}:\)

\(CH^2+MH^2=MC^2\left(Đlpytago\right)\)

\(\Rightarrow CH^2=MC^2-MH^2\)

\(\Rightarrow CH^2-BH^2=MC^2-MH^2-BH^2\)

\(\Rightarrow CH^2-BH^2=MC^2-\left(MH^2+BH^2\right)\)

\(\Rightarrow CH^2-BH^2=MC^2-MB^2\left(\Delta MHB\perp\text{tại H,MB^2}=MH^2+BH^2\left(pytago\right)\right)\)

\(\Rightarrow CH^2-BH^2=AC^2\)\(\left(\Delta AMC\perp\text{tại A},MC^2-MA^2=AC^2\left(PYTAGO\right)\right)\)

Từ A hạ AK ⊥BC( AK∈ BC)

{AK⊥BCMN⊥BC{AK⊥BCMN⊥BC

⇒AK//MN

=>NBKNNBKN=MBMAMBMA=1

=>KN=NB

Xét Δ vuông CAK và Δ ABC

AKCˆAKC^=CABˆCAB^=90o

AKCˆAKC^=ACBˆACB^

=> Δ CKA đồng dạng với Δ CAB

=>CACBCACB=CKCACKCA⇔CA2=CB.CK

=>CA2= (CN+NB)(CN-NB)

=CN2-NB2(đpcm)

hvvvg

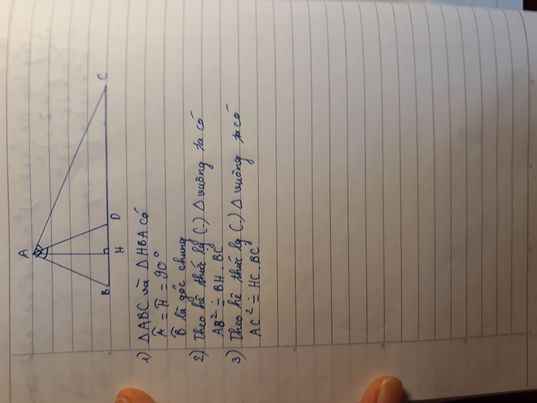
1: Xét ΔABC vuông tại A và ΔHBA vuông tại H có 

\(\widehat{B}\) chung

Do đó: ΔABC\(\sim\)ΔHBA

2: Ta có: ΔABC\(\sim\)ΔHBA

nên \(\dfrac{BA}{BH}=\dfrac{BC}{BA}\)

hay \(AB^2=BH\cdot BC\)

3: Xét ΔACH vuông tại H và ΔBCA vuông tại A có 

\(\widehat{C}\) chung

Do đó: ΔACH\(\sim\)ΔBCA

Suy ra: \(\dfrac{CA}{CB}=\dfrac{CH}{CA}\)

hay \(CA^2=CH\cdot CB\)

1: Xét ΔABH vuông tại H và ΔCBA vuông tại A có 

\(\widehat{B}\) chung

Do đó: ΔABH\(\sim\)ΔCBA

2: Ta có: ΔABH\(\sim\)ΔCBA

nên \(\dfrac{BA}{BC}=\dfrac{BH}{BA}\)

hay \(BA^2=BH\cdot BC\)

ho tam giác vg ác vg tạo a (ab<ac) ,đường cao ah. Trên bc lấy m sao cho ba=bm. Từ m kẻ mn vg góc với ac (n thuộc ac). Cmr

a. Tam giác ANH cân

b. BC +AH >AB+AC

c. 2ac^2 - bc^2= ch^2- bh^2

o l m . v n

a: Xet ΔAHD vuông tại H và ΔAKD vuông tại K co

AD chung

góc HAD=góc KAD

=>ΔAHD=ΔAKD

b: góc BAD+góc CAD=90 độ

góc BDA+góc DAH=90 độ

góc CAD=góc DAH

=>góc BAD=góc BDA
=>ΔBAD cân tại B

a: Xét ΔABC có AB<AC
mà HB,HC lần lượt là hình chiếu của AB,AC

nên HB<HC

b: Xét ΔMBC có

HB,HC lần lượt là hình chiếu của MB,MC trên BC

HB<HC

=>MB<MC

a) Xét \(\Delta ABC\) và \(\Delta HBA\) có \(\widehat{BAC}=\widehat{BHA}=90^o;\widehat{B}-\text{góc chung}\)

\(\Rightarrow \Delta ABC\sim\Delta HBA(g.g)\)

\(\Rightarrow\dfrac{AB}{BC}=\dfrac{HB}{BA}\Rightarrow AB^2=BH.BC\)

b) Tương tự câu a

c) Ta có \(AB.AC=2S_{ABC}=AH.BC\)

1: Xét ΔABC vuông tại A và ΔHBA vuông tại H có

\(\widehat{B}\) chung

Do đó: ΔABC\(\sim\)ΔHBA

2: Ta có: ΔABC\(\sim\)ΔHBA

nên \(\dfrac{AB}{HB}=\dfrac{CB}{AB}\)

hay \(AB^2=HB\cdot BC\)