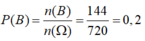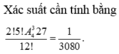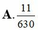Số cách xếp ngẫu nhiên 12 học sinh thành hàng ngang là 12! cách.

Ta tìm số cách xếp thoả mãn:

Xếp hai bạn An và Bình cạnh nhau có 2! cách, gọi nhóm này là X;

Xếp 4 bạn lớp C còn lại cùng với X có 5! cách;

Lúc này có 4 vị trí (xen giữa các bạn lớp C còn lại và X) để xếp 3 bạn lớp B vào có A34A43cách;

Còn lại 3 vị trí để các bạn lớp A có thể xếp vào (1 vị trí xen giữa và ở hai đầu) có 3.3.3 cách.

Vậy có tất cả 2 ! 5 ! A 4 3 27  cách xếp thoả mãn.

Xác suất cần tính bằng  2 ! 5 ! A 4 3 27 12 ! = 1 3080

Chọn đáp án D.

Chọn A

Gọi A là biến cố: Xếp hai học sinh A, B ngồi ở hai bàn xếp cạnh nhau.

Số cách xếp ngẫu nhiên  học sinh vào 36 cái bàn là 36!, 

Ta tìm số cách xếp thuận lợi cho biến cố :

     - Chọn 1 hàng hoặc 1 cột có C 12 1  cách;

- Mỗi hàng hoặc cột đều có 6 bàn nên có 5 cặp bàn xếp kề nhau, chọn lấy 1 trong 5 cặp bàn cạnh nhau trong hàng hoặc cột vừa chọn ra có C 5 1  cách;

- Xếp A và B vào cặp bàn vừa chọn có 2! cách;

- Xếp 34 học sinh còn lại có 34! cách.

Vậy tổng số cách xếp thoả mãn là: 

Vậy xác suất cần tính: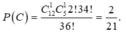 

Chọn đáp án A.

Chọn B

  `n(\Omega)=6! =720`

`@TH1:` H/s lớp `C` ngồi đầu tiên hoặc cuối cùng.

  `=>` Có `2.1.A_3 ^1 .4! =144` cách xếp h/s lớp `C` không ngồi cạnh lớp `B`.

`@TH2:` H/s lớp `C` không ngồi đầu cũng không ngồi cuối.

  `=>` Có `4.A_3 ^2 .3! =144` cách xếp h/s lớp `C` không ngồi cạnh lớp `B`.

Gọi `A:`" H/s lớp `C` không ngồi cạnh h/s lớp `B`"

   `=>n(A)=144.2=288`

`=>P(A)=288/720=2/5`

    `->bb D`

Không gian mẫu là việc sắp xếp 6 bạn vào 6 ghế tùy ý

⇒ n(Ω) = P6 = 6! = 720.

a. Gọi A: “ Nam, nữ ngồi xen kẽ nhau”

+ Chọn chỗ ngồi cho 3 bạn nữ: Có 2 cách (Vị trí 1,3,5 hoặc 2,4,6).

+ Sắp xếp 3 bạn nữ vào 3 chỗ: Có 3! = 6 cách

+ Sắp xếp 3 bạn nam vào 3 chỗ còn lại: Có 3! = 6 cách

⇒ Theo quy tắc nhân: n(A) = 2.6.6 = 72 (cách).

⇒ n(A) = 2.3!.3! = 72

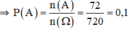
b. B: “Ban bạn nam ngồi cạnh nhau”

+ Chọn 3 chỗ ngồi cạnh nhau cho 3 bạn nam: Có 4 cách.

+ Sắp xếp 3 bạn nam vào 3 chỗ: Có 3! = 6 cách.

+ Sắp xếp 3 bạn nữ vào 3 chỗ còn lại: Có 3! = 6 cách

⇒ Theo quy tắc nhân: n(B) = 4.6.6 = 144 (cách)

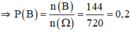
Xác suất để ba bạn nam ngồi cạnh nhau là: