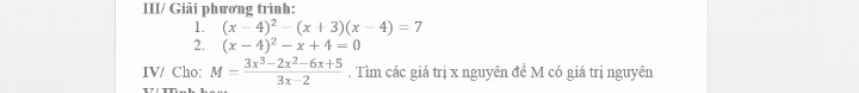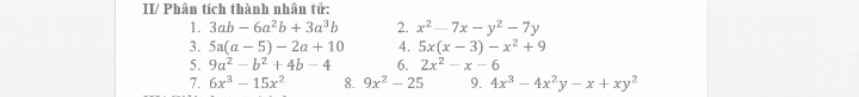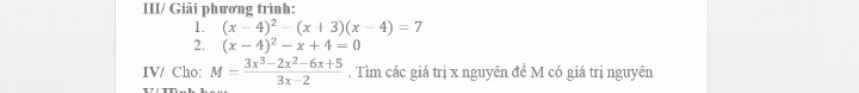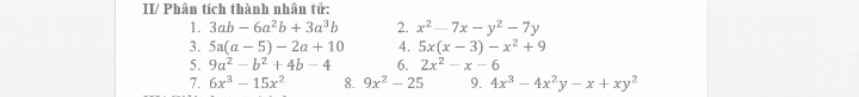\(1,\Leftrightarrow x^2-8x+16-x^2+x+12=7\\ \Leftrightarrow-7x=-21\\ \Leftrightarrow x=3\\ 2,\Leftrightarrow\left(x-4\right)^2-\left(x-4\right)=0\\ \Leftrightarrow\left(x-4\right)\left(x-5\right)=0\Leftrightarrow\left[{}\begin{matrix}x=4\\x=5\end{matrix}\right.\)

\(1,=3ab\left(1-2a+b\right)\\ 2,=\left(x-y\right)\left(x+y\right)-7\left(x+y\right)=\left(x+y\right)\left(x-y-7\right)\\ 3,=\left(a-5\right)\left(5a-2\right)\\ 4,=5x\left(x-3\right)-\left(x-3\right)\left(x+3\right)=\left(x-3\right)\left(4x-3\right)\\ 5,=9a^2-\left(b-2\right)^2=\left(3a-b+2\right)\left(3a+b-2\right)\\ 6,=2x^2-4x+3x-6=\left(x-2\right)\left(2x+3\right)\\ 7,=3x^2\left(2x-5\right)\\ 8,=\left(3x-5\right)\left(3x+5\right)\\ 9,=4x^2\left(x-y\right)-x\left(x-y\right)=x\left(4x-1\right)\left(x-y\right)\)

3.

\(4sinx+cosx+2cos\left(x+\dfrac{\pi}{3}\right)=2\)

\(\Leftrightarrow4sinx+cosx+cosx-\sqrt{3}sinx=2\)

\(\Leftrightarrow\left(4-\sqrt{3}\right)sinx+2cosx=2\)

\(\Leftrightarrow\sqrt{23-4\sqrt{3}}\left(\dfrac{4-\sqrt{3}}{\sqrt{23-4\sqrt{3}}}sinx+\dfrac{2}{\sqrt{23-4\sqrt{3}}}cosx\right)=2\)

\(\Leftrightarrow cos\left(x-arccos\dfrac{2}{\sqrt{23-4\sqrt{3}}}\right)=\dfrac{2}{\sqrt{23-4\sqrt{3}}}\)

\(\Leftrightarrow x-arccos\dfrac{2}{\sqrt{23-4\sqrt{3}}}=\pm arccos\dfrac{2}{\sqrt{23-4\sqrt{3}}}+k2\pi\)

\(\Leftrightarrow\left[{}\begin{matrix}x=2arccos\dfrac{2}{\sqrt{23-4\sqrt{3}}}+k2\pi\\x=k2\pi\end{matrix}\right.\)

4.

\(sinx+2cos\left(x+\dfrac{\pi}{3}\right)+4sin\left(x+\dfrac{\pi}{6}\right)+cosx=4\)

\(\Leftrightarrow sinx+cosx-\sqrt{3}sinx+2\sqrt{3}sinx+2cosx+cosx=4\)

\(\Leftrightarrow\left(1+\sqrt{3}\right)sinx+4cosx=4\)

\(\Leftrightarrow\sqrt{20+2\sqrt{3}}\left(\dfrac{1+\sqrt{3}}{\sqrt{20+2\sqrt{3}}}sinx+\dfrac{4}{\sqrt{20+2\sqrt{3}}}cosx\right)=4\)

\(\Leftrightarrow cos\left(x-arccos\dfrac{4}{\sqrt{20+2\sqrt{3}}}\right)=\dfrac{4}{\sqrt{20+2\sqrt{3}}}\)

\(\Leftrightarrow x-arccos\dfrac{4}{\sqrt{20+2\sqrt{3}}}=\pm arccos\dfrac{4}{\sqrt{20+2\sqrt{3}}}+k2\pi\)

\(\Leftrightarrow\left[{}\begin{matrix}x=2arccos\dfrac{4}{\sqrt{20+2\sqrt{3}}}+k2\pi\\x=k2\pi\end{matrix}\right.\)

Câu 58: B

Câu 59: C