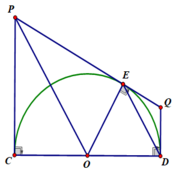
Cho đường tròn ( O) có đường kính CD = 2R. Vẽ hai tiếp tuyến Cx, Dy với đường tròn. Qua K bất kì trên đường tròn (O) (K khác C, D )vẽ tiếp tuyến thứ ba với đường tròn cắt Cx, Dy lần lượt tại M, N. Gọi E là giao điểm của DK và Cx.
a) Chứng minh: MC + ND = MN và CK ^ DE ?
b) Kẻ KH vuông CD. Chứng minh : CH.CD=KD.KE
c) Chứng minh: CM.DN = R² và tính MON.