Câu 7 giúp mình với ạ :((
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Ta có:
\(cos20^0=sin70^0\)
\(cos55^0=sin35^0\)
\(\)Lại có:\(sin\alpha< tan\alpha\)
=> \(sin35^0< sin38^0< sin70^0< sin88^0< tan48^0\)
=> \(cos55^0< sin38^0< cos20^0< sin88^0< tan48^0\)


Ta có: \(n_{CO_2}=\dfrac{8,96}{22,4}=0,4\left(mol\right)\)
\(n_{H_2O}=\dfrac{10,8}{18}=0,6\left(mol\right)\)
⇒ nH2O > nCO2 → X là ankan.
Vậy: X là metan.
nCO2 = 8,96/22,4 = 0,4 mol
nH2O = 10,8/18 = 0,6 mol
Đốt cháy C2H4 thu được nCO2 = nH2O:
C2H4 + 3O2 -> (nhiệt độ) 2CO2 + 2H2O
Mà nH2O > nCO2 nên X phải là hidrocacbon chỉ chứa liên kết đơn
Vậy chỉ có metan (CH4) thoả mãn.

7)Đk \(x\le2\)
Pt \(\Leftrightarrow x^2-x+8=4-2x\)
\(\Leftrightarrow x^2+x+4=0\)
\(\Delta=-15< 0\) => vô nghiệm
Vậy pt vô nghiệm
10) \(\sqrt{9x+9}-4\sqrt{\dfrac{x+1}{4}}=5\) (đk: \(x\ge-1\)
\(\Leftrightarrow\sqrt{\left(x+1\right).9}-\dfrac{4\sqrt{x+1}}{\sqrt{4}}=5\)
\(\Leftrightarrow3\sqrt{x+1}-2\sqrt{x+1}=5\)
\(\Leftrightarrow\sqrt{x+1}=5\) \(\Leftrightarrow x=24\) (tm)
Vậy \(S=\left\{24\right\}\)

Câu 7
\(b,\) Thể 1 nhiễm : \(2n+1\)\(=14+1=15\)
Thể 3 nhiễm : \(2n+1+1+1=14+1+1+1=17\)
Thể tam bội : \(3n=3.7=21\)
Thể tứ bội : \(4n=7.4=28\)
Câu 7
- Sai vì phép lai phân tích là phép lai giữa cá thể mang tính trang trội cần xác định kiểu gen với cá thể mang tính trạng lặn để kiểm tra kiểu gen của cơ thể mang tính trạng trội. (đã sửa)
- Đúng vì \(6.2^5=192\left(tb\right)\)
- Sai vì ở kì giữa của quá trình nguyên phân, các NST kép đóng xoắn cực đại xếp thành 1 hàng trên mặt phẳng xích đạo của thoi phân bào .

\(L=3060A^o\) \(\Rightarrow N=\dfrac{2L}{3,4}=\dfrac{2\cdot3060}{3,4}=1800\left(nu\right)\)
Mà \(2A+2G=1800\) \(\Rightarrow\left\{{}\begin{matrix}A=T=438nu\\G=X=462\left(nu\right)\end{matrix}\right.\)
Khối lượng đoạn gen trên:
\(M=N\cdot300=1800\cdot300=540000\left(đvC\right)\)





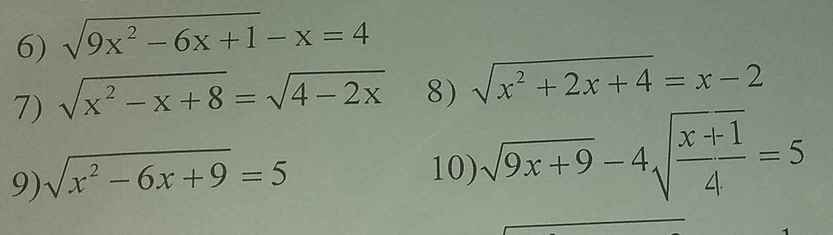



Câu 1:
a: \(=2x^4-6x^2\)
b: \(=3y^2+2\)
Câu 1:
\(a,=2x^4-6x^2\\ b,=3y^2+2\)
Câu 2:
\(\widehat{C}=360^0-55^0-80^0-120^0=105^0\\ \Rightarrow\text{Góc ngoài tại }\widehat{C}=180^0-105^0=75^0\)
Câu 3:
\(a,AM=\dfrac{BC}{2}=\dfrac{\sqrt{AB^2+AC^2}}{2}=\dfrac{15}{2}\left(cm\right)\\ b,S_{ABC}=\dfrac{1}{2}AB\cdot AC=\dfrac{1}{2}\cdot12\cdot9=54\left(cm^2\right)\)
Câu 4:
\(a,=\dfrac{x^2-4x+4}{x-2}=\dfrac{\left(x-2\right)^2}{x-2}=x-2\\ b,=\dfrac{x+1+2x+3-4+x}{6x^2y}=\dfrac{4x}{6x^2y}=\dfrac{2}{3xy}\)