3:4 =3/4

=> số bé 3 phần, số lớn 4 phần

Tỉ số của chúng bằng 3 : 4 là 3 / 4

Vậy số bé bằng 3/4 số lớn

Số bé là :

     108 : ( 3 * 4 ) * 3 = 27 

Số lớn là :

     108 - 27 = 81

              Đáp số : 27 và 81

gọi số bé là 3a số lớn là 7a

ta có 3a.7a=525

=>21a^2=525

=>a^2=525:21=25=>a=5=>số bé bằng 5.3=15

số lớn bằng 5.7=35

GỌi 2 số cần tìm là:a và b

Theo đề bài ta có:

\(\frac{a}{b}=\frac{1}{4};a.b=16\)

\(\frac{a}{b}=\frac{1}{4}\Leftrightarrow a=\frac{1}{4}b\)

Thay \(a=\frac{1}{4}b\)vào \(a.b=16\)ta được:

      \(\frac{1}{4}b.b=16\)

\(\Leftrightarrow\frac{1}{4}b^2=16\)

\(\Leftrightarrow b^2=64\)

\(\Leftrightarrow\orbr{\begin{cases}b=8\\b=-8\end{cases}}\)

Thay b=8 vào \(a.b=16\)ta được:\(8a=16\Leftrightarrow a=2\)

Thay b=-8 vào \(a.b=16\)ta được:\(\left(-8\right)a=16\Leftrightarrow a=-2\)

Vậy (a,b)\(\in\left\{\left(2,8\right);\left(-2,-8\right)\right\}\)

KO biết

Gọi hai số cần tìm là m và n. Ta có: 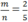 và mn = 40.

Vì 

Suy ra: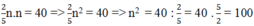 

Vì n2 = 100 nên n = 10 hoặc n = -10

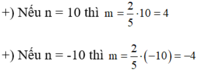
Vậy hai số cần tìm là m = 4 , n = 10 hoặc m = -4 , n = -10

Gọi hai số cần tìm lần lượt là a và Theo đầu bài ta có : \(\frac{a}{b}=\frac{3}{7}\) và a . b = 189 ( \(a,b\) \(\in Z,b\ne0\))\(\frac{a}{b}=\frac{3}{7}\)nên a = 3x , b = 7x (\(x\in Z,x\ne0\))

Do đó : a . b = 189

3x . 7x = 189

x . x = 189 : ( 3 . 7 )

x² = 9

x² = (\(\pm3\))²

x = \(\left(\pm3\right)^2\)

x = \(\pm3\)

Nếu x = 3 thì a = 3 . 3 = 9 , b = 7 . 3 = 21.

Nếu x = -3 thì a = 3 . (-3) = -9 , b = 7 . (-3) = -21.

\(\)

9 va 21

ba​=52​ nên a = 2k , b = 5k (k\inℤ,k\ne0)(k∈Z,k̸​=0)

Từ a . b = 40 \Rightarrow2k\cdot5k=40⇒2k⋅5k=40

\Rightarrow k^2=40:(2\cdot5)⇒k2=40:(2⋅5)

\Rightarrow k^2=40:10⇒k2=40:10

\Rightarrow k^2=4\Rightarrow k=\pm2⇒k2=4⇒k=±2

Vậy : a = 4              b = 10            (k=2)(k=2)

         a = -4             b = -10           (k=-2)(k=−2)

\(\frac{a}{b}=\frac{2}{5}\) nên a = 2k , b = 5k \((k\inℤ,k\ne0)\)

Từ a . b = 40 \(\Rightarrow2k\cdot5k=40\)

\(\Rightarrow k^2=40:(2\cdot5)\)

\(\Rightarrow k^2=40:10\)

\(\Rightarrow k^2=4\Rightarrow k=\pm2\)

Vậy : a = 4              b = 10            \((k=2)\)

         a = -4             b = -10           \((k=-2)\)