Cho tam giác ABC có AB = 6cm, AC = 9cm. Trên cạnh AB lấy M sao cho AM = 4,5cm, trên cạnh AC lấy N sao cho AN = 3cm.
a) So sánh các tỉ số AN/AB và AM/AC. Chứng minh : Tam giác ANM đồng dạng tam giác ABC.
b) Kẻ MK // BC (K thuộc AC). Tính CK và NK.
c) Trên cạnh BC lấy điểm J sao cho BC = 3CJ, trên cạnh MN lấy điểm I sao cho 3MI = MN. Chứng minh : tam giác AMI đồng dạng tam giác ACJ.
d) Vẽ điểm F sao cho A là trung điểm của FB. Gọi AD, AE lần lượt là đường phân giác của tam giác ABC, tam giác AFC (D thuộc BC, E thuộc FC). Chứng minh : ED // FB

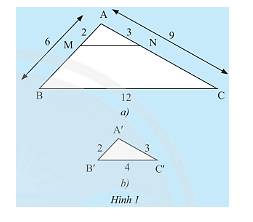
a) Ta có: \(\dfrac{AN}{AB}=\dfrac{3}{6}=\dfrac{1}{2}\)
\(\dfrac{AM}{AC}=\dfrac{4.5}{9}=\dfrac{1}{2}\)
Do đó: \(\dfrac{AN}{AB}=\dfrac{AM}{AC}\)\(\left(=\dfrac{1}{2}\right)\)
Xét ΔANM và ΔABC có
\(\dfrac{AN}{AB}=\dfrac{AM}{AC}\)(cmt)
\(\widehat{BAC}\) chung
Do đó: ΔANM\(\sim\)ΔABC(c-g-c)