\(h\left(x\right)=x^2-4x+5+m\)

\(g\left(x\right)=\left|h\left(x\right)\right|=\left|f\left(x\right)+m\right|=\left|x^2-4x+5+m\right|\)

\(h\left(0\right)=5+m;h\left(4\right)=5+m;h\left(2\right)=1+m\)

TH1: \(1+m>0\Leftrightarrow m>-1\)

\(max=5+m=9\Leftrightarrow m=4\left(tm\right)\)

TH2: \(5+m< 0\Leftrightarrow m< -5\)

\(max=-1-m=9\Leftrightarrow m=-10\left(tm\right)\)

TH3: \(5+m>0>1+m\Leftrightarrow-5< m< -1\)

Nếu \(5+m< -1-m\Leftrightarrow m< -3\)

\(max=-1-m=9\Leftrightarrow m=-10\left(tm\right)\)

Nếu \(5+m=-1-m\Leftrightarrow m=-3\)

\(max=5+m=2\ne9\)

\(\Rightarrow m=-3\) không thỏa mãn yêu cầu bài toán

Nếu \(5+m>-1-m\Leftrightarrow m>-3\)

\(max=5+m=9\Leftrightarrow m=4\left(tm\right)\)

Vậy \(m=4;m=-10\)

\(g'\left(x\right)=0\Rightarrow x=0\)

Ta thấy \(g\left(x\right)\) đồng biến trên \(\left(0;+\infty\right)\)

\(\Rightarrow g\left(f\left(x\right)\right)\) đồng biến khi \(f\left(x\right)\ge0\)

\(\Rightarrow g\left(f\left(x\right)\right)\) đồng biến trên \(\left(3;+\infty\right)\) khi \(f\left(x\right)\ge0\) ; \(\forall x>3\)

\(\Leftrightarrow x^2-4x\ge-m\) ; \(\forall x>3\)

\(\Leftrightarrow-m\le\min\limits_{x>3}\left(x^2-4x\right)\)

\(\Rightarrow-m\le-3\Rightarrow m\ge3\)

\(y=\left(x+2\right)\left(3-x\right)\)

\(=3x-x^2+6-2x\)

\(=-x^2+x+6\)

=>y'=-2x+1

Đặt y'=0

=>-2x+1=0

=>-2x=-1

=>\(x=\dfrac{1}{2}\)

\(f\left(\dfrac{1}{2}\right)=\left(\dfrac{1}{2}+2\right)\left(3-\dfrac{1}{2}\right)=\dfrac{5}{2}\cdot\dfrac{5}{2}=\dfrac{25}{4}\)

\(f\left(-2\right)=\left(-2+2\right)\left(3+2\right)=0\)

\(f\left(3\right)=\left(3+2\right)\left(3-3\right)=0\)

=>\(y_{max\left[-2;3\right]}=\dfrac{25}{4}\)

Chọn B

a.

\(y=x^2\left(4-2x\right)=x.x.\left(4-2x\right)\le\left(\dfrac{x+x+4-2x}{3}\right)^3=\dfrac{64}{27}\)

\(y_{max}=\dfrac{64}{27}\) khi \(x=4-2x\Rightarrow x=\dfrac{4}{3}\)

b.

\(y=x\left(2-x\right)^2=\dfrac{1}{2}.2x.\left(2-x\right)\left(2-x\right)\le\dfrac{1}{2}\left(\dfrac{2x+2-x+2-x}{3}\right)^3=\dfrac{32}{27}\)

\(y_{max}=\dfrac{32}{27}\) khi \(2x=2-x\Rightarrow x=\dfrac{2}{3}\)

2.

\(I=\int e^{3x}.3^xdx\)

Đặt \(\left\{{}\begin{matrix}u=3^x\\dv=e^{3x}dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=3^xln3dx\\v=\dfrac{1}{3}e^{3x}\end{matrix}\right.\)

\(\Rightarrow I=\dfrac{1}{3}e^{3x}.3^x-\dfrac{ln3}{3}\int e^{3x}.3^xdx=\dfrac{1}{3}e^{3x}.3^x-\dfrac{ln3}{3}.I\)

\(\Rightarrow\left(1+\dfrac{ln3}{3}\right)I=\dfrac{1}{3}e^{3x}.3^x\)

\(\Rightarrow I=\dfrac{1}{3+ln3}.e^{3x}.3^x+C\)

1.

\(I=\int\left(2x-1\right)e^{\dfrac{1}{x}}dx=\int2x.e^{\dfrac{1}{x}}dx-\int e^{\dfrac{1}{x}}dx\)

Xét \(J=\int2x.e^{\dfrac{1}{x}}dx\)

Đặt \(\left\{{}\begin{matrix}u=e^{\dfrac{1}{x}}\\dv=2xdx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=-\dfrac{e^{\dfrac{1}{x}}}{x^2}dx\\v=x^2\end{matrix}\right.\)

\(\Rightarrow J=x^2.e^{\dfrac{1}{x}}+\int e^{\dfrac{1}{x}}dx\)

\(\Rightarrow I=x^2.e^{\dfrac{1}{x}}+C\)

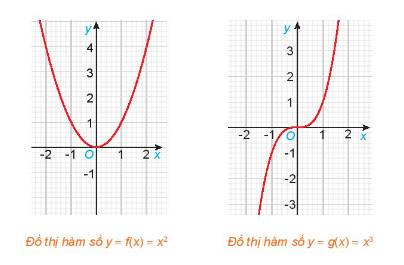
a) Tập xác định của hàm số đã cho là: \({D_f} = \mathbb{R};\;{D_g} = \mathbb{R}\)

b) Ta có: \(f\left( { - x} \right) = {\left( { - x} \right)^2} = {x^2} = f\left( x \right)\)

Đồ thị của hàm số \(y = f\left( x \right) = {x^2}\) đối xứng qua trục tung

c) Ta có: \(g\left( { - x} \right) = {\left( { - x} \right)^3} =  - {x^3} =  - g\left( x \right)\)

Đồ thị của hàm số \(y = g\left( x \right) = {x^3}\) đối xứng qua gốc tọa độ