Đáp án đúng : A

Chọn A

Có cách chia 20 bạn vào 4 nhóm, mỗi nhóm 5 bạn.

- Gọi A là biến cố “ 5 bạn nữ vào cùng một nhóm”

- Xét 5 bạn nữ thuộc nhóm A có cách chia các bạn nam vào các nhóm còn lại. 

- Do vai trò các nhóm như nhau nên có

Khi đó .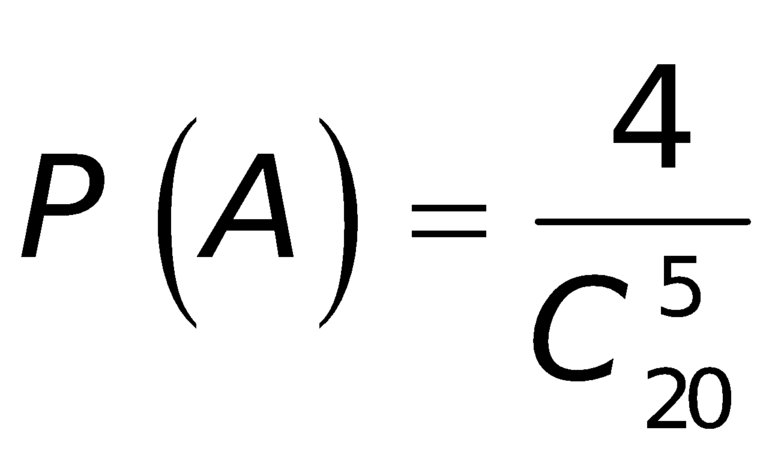

Gọi X là biến cố " chia 20 bạn thành 4 nhóm A, B, C, D mỗi nhóm 5 bạn sao cho 5 bạn nữ thuộc cùng 1 nhóm"

Ta có \(\left|\Omega\right|=C^5_{20}C^5_{10}C^5_5\) cách chia các bạn nam vào 3 nhóm còn lại.

Do vai trò các nhóm như nhau, có \(4C^5_{20}C^5_{10}C^5_5\) cách chia các bạn vào các nhóm A, B, C,D trong đó 5 bạn nữ thuộc một nhóm

Xác suất cần tìm là \(P\left(X\right)=\frac{4}{C^5_{20}}=\frac{1}{3876}\)

Số cách chia 14 tiết mục thành 2 nhóm là: \(n(\Omega )= C_{14}^{7}.C_{7}^{7} \)

Gọi A là biến cố 2 tiết mục của lớp 12a1 được biểu diễn cùng một nhóm.

Số cách chọn 1 trong 2 nhóm để xếp 2 tiết mục của lớp 12a1 vào là: \( C_{2}^{1}\)

Số cách xếp 12 tiết mục còn lại là: \(C_{12}^{5}.C_{7}^{7}\)

Ta có \(n(A)= C_{2}^{1}.C_{12}^{5}.C_{7}^{7} \)

Xác suất xảy ra A là: \(P(A)= \frac{n(A)}{n(\Omega )} = \frac{C_{2}^{1}.C_{12}^{5}.C_{7}^{7}}{C_{14}^{7}.C_{7}^{7} } = \frac{6}{13} \)

ban tổ chúc có số cách chọn 

TH1 bạn tốt đc giải nhất

1!x4P1

TH2 bạn Tốt đc giải nhì

1!x4P1

--> só cách chọn là 8 ( cách)

đây là cách nghĩ của mk bạn xe mcos chuẩ nko nhé

Cảm ơn bạn

(+) Vòng đầu có 4 đội mỗi bảng

=> Mỗi nhóm có 8 bảng

Nhận xét : Mỗi nhóm sẽ phải đấu với 3 nhóm còn lại tạo thành 3 trận đấu

=> Có : 3 . 4 = 12 ( trân trong mỗi nhóm )

Trên thực tế số trận này đã được tính 2 lần

=> Số trận thực trong mỗi bảng là : 12 : 2 = 6 ( trận )

=> Có số trận là : 6 x 8 = 48

(+) Vòng 2 sẽ mỗi bảng sẽ loại 2

=> Còn lại 16 đôi .

=> Có 4 bảng

Nhận xét : Mỗi nhóm sẽ phải đấu với 3 nhóm còn lại tạo thành 3 trận đấu

=> Có : 3 . 4 = 12 ( trân trong mỗi nhóm )

Trên thực tế số trận này đã được tính 2 lần

=> Số trận thực trong mỗi bảng là : 12 : 2 = 6 ( trận )

=> Có số trận là : 6 x 4 = 24

(+) Vòng 3 sẽ mỗi bảng sẽ loại 2

=> Còn lại 8 đôi .

=> Có 2 bảng

Nhận xét : Mỗi nhóm sẽ phải đấu với 3 nhóm còn lại tạo thành 3 trận đấu

=> Có : 3 . 4 = 12 ( trân trong mỗi nhóm )

Trên thực tế số trận này đã được tính 2 lần

=> Số trận thực trong mỗi bảng là : 12 : 2 = 6 ( trận )

=> Có số trận là : 6 x 2 = 12

(+) Vòng 4 sẽ cồn lại 4 đội .

=> Có 3 trận

Vậy giải dấu có số trận là : 48 + 24 + 12 + 3 = 87 ( trận )

*) Trong mỗi nhóm 4 đội, các đội thi đấu vòng tròn, mỗi đội đấu với 3 đội còn lại, 4 đội sẽ có 4 x 3 = 12 trận, tuy nhiên mỗi trận được tính 2 lần, vì vậy có 12 : 2 = 6 trận trong mỗi nhóm.

Sau mỗi vòng, mỗi nhóm chỉ 2 đội vào và 2 đội bị loại, như vậy số đội vòng sau giảm đi một nửa so với số đội vòng trước.

*) Vòng thứ nhất:

Số đội tham gia thi đấu là: 32 đội

Số nhóm là: 32 : 4 = 8 (nhóm)

Số trận đấu là: 8 x 6 = 48 (trận)

Vòng thứ hai:

Số đội tham gia thi đấu còn là: 32 : 2 = 16 (đội)

Số nhóm là: 16 : 4 = 4 (nhóm)

Số trận đấu là: 4 x 6 = 24 (trận)

Vòng thứ ba:

Số đội tham gia thi đấu còn là: 16 : 2 = 8 (đội)

Số nhóm là: 8 : 4 = 2 (nhóm)

Số trận đấu là: 2 x 6 = 12 (trận)

Vòng thứ tư:

Số đội tham gia thi đấu còn là: 8 : 2 = 4 (đội)

Số nhóm là: 4 : 4 = 1 (nhóm)

Số trận đấu là: 1 x 6 = 6 (trận)

Sau vòng thứ tư (vòng cuối), chọn hai đội nhất nhì để thi đấu thêm 1 trận chung kết.

Tổng cộng số trận đấu là:

48 + 24 + 12 + 6 + 1 = 91 (trận)

Đáp số: 91 trận

nam hỏi bình :" tớ vùa viết xong 20 số lẻ liên tiếp có tổng là 40020 . tớ đó cậu tìm dược số lớn nhất trong 20 số lẻ đó toán tuổi thơ 5