a) Gọi O là tâm đường tròn ngoại tiếp. Do tam giác ABC là tam giác đều nên O đồng thời là trọng tâm tam giác đều ABC.

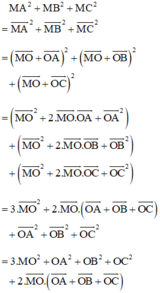
Lại có:

+ O là trọng tâm tam giác nên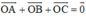 

+ Bán kính đường tròn ngoại tiếp tam giác:

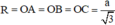
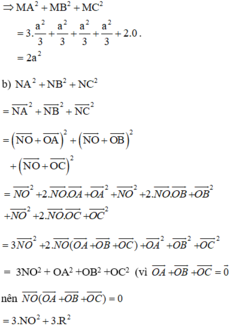
Ta có: NA2 + NB2 + NC2 ngắn nhất

⇔ NO2 ngắn nhất vì R không đổi

⇔ NO ngắn nhất

⇔ N là hình chiếu của O trên d.

Em tham khảo link này nhé!

Câu hỏi của channel Anhthư - Toán lớp 7 - Học toán với OnlineMath

Đáp án C.

Gắn hệ trục tọa độ Oxyz, với O(0;0;0) là trung điểm của AB => OC=  3

Khi đó 

⇒ x 2 + ( y + 1 ) 2 + z 2 + x 2 + ( y - 1 ) 2 + z 2 + 2 ( x - 3 ) 2 + 2 y 2 + 2 z 2 = 12

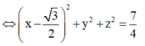
Vậy tập hợp các điểm M là một mặt cầu có bán kính  R = 7 2

bạn chơi bang bang ak mà chụp hình ảnh kiếm thần nên có nick bang bang cho mình một nick nhé mình giải bài này cho

Câu hỏi của channel Anhthư - Toán lớp 7 - Học toán với OnlineMath

Em tham khảo nhé!

Phía nửa mặt phẳng bờ AB không chứa M lấy điểm N sao cho AMN là tam giác đều

Ta có ˆCAB=ˆMANCAB^=MAN^

<=>ˆCAM+ˆMAB=ˆMAB+ˆBANCAM^+MAB^=MAB^+BAN^

<=>ˆCAM=ˆBANCAM^=BAN^ (1)

mà CA =BA và AM =AN (2)

từ (1, 2) =>△CAM=△BAN△CAM=△BAN (c, g, c) (3)

(3) =>CM =BN

ta có MA2=MB2+MC2MA2=MB2+MC2

<=>MN2=MB2+BN2MN2=MB2+BN2

=>t giác MBN vuông tại B

(3) =>ˆACM=ˆABNACM^=ABN^

ˆMBN=ˆABM+ˆABN=90∘MBN^=ABM^+ABN^=90∘

<=>ˆABM+ˆACM=90∘ABM^+ACM^=90∘

<=>(60∘−ˆMBC)+(60∘−ˆMCB)=90∘(60∘−MBC^)+(60∘−MCB^)=90∘

<=>ˆMBC+ˆMCB=30∘MBC^+MCB^=30∘

<=>ˆBMC=180∘−30∘=150∘

thankinhachi

thưa ... bạn ... mình ... chịu

mk ko bt lm câu b nha ~ xl

c,Vẽ tam giác đều AMD ( D thuộc nửa mặt phẳng bờ AM không chứa C)(Bạn tự vẽ hình nha, dễ như ăn kẹo ấy)

=> DM = AD = AM

Sau đó bạn chứng minh tam giác ADB = tam giác AMC (c.g.c) (cũng dễ thôi)

=> BD = MC (cặp cạnh tương ứng)

Ta có: DM = AM, BD = MC

=> DM : BM : BD = 3:4:5

=> tam giác BDM vuông tại M

=> góc AMB = 90o + 60o = 150o