\(B\left(1;1\right);C\left(2;4\right)\)

Gọi pt đường thẳng BC có dạng: \(y=ax+b\)

\(\Rightarrow\left\{{}\begin{matrix}a+b=1\\2a+b=4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=3\\b=-2\end{matrix}\right.\) \(\Rightarrow y=3x-2\)

Gọi M và N lần lượt là giao điểm của đường thẳng BC với Ox và Oy

\(\Rightarrow M\left(\dfrac{2}{3};0\right)\) ; \(N\left(0;-2\right)\) \(\Rightarrow\left\{{}\begin{matrix}OM=\dfrac{2}{3}\\ON=2\end{matrix}\right.\)

Gọi H là chân đường vuông góc hạ từ O xuống MN \(\Rightarrow OH\) là k/c từ O tới BC

Áp dụng hệ thức lượng:

\(\dfrac{1}{OH^2}=\dfrac{1}{OM^2}+\dfrac{1}{ON^2}=\dfrac{5}{2}\Rightarrow OH=\dfrac{\sqrt{10}}{5}\)

a) Vì A, B thuộc (P) nên:

x A = − 1 ⇒ y A = 1 2 ⋅ - 1 2 = 1 2 x B = 2 ⇒ y B = 1 2 ⋅ 2 2 = 2 ⇒ A − 1 ; 1 2  ,  B ( 2 ; 2 )

b) Gọi phương trình đường thẳng (d) là y = ax + b.

Ta có hệ phương trình:

− a + b = 1 2 2 a + b = 2 ⇔ 3 a = 3 2 2 a + b = 2 ⇔ a = 1 2 b = 1

Vậy (d):  y = 1 2 x + 1 .

c) (d) cắt trục Oy tại điểm C(0; 1) và cắt trục Ox tại điểm D(– 2; 0)

=>  OC = 1 và OD = 2

Gọi h là khoảng cách từ O tới (d).

Áp dụng hệ thức về cạnh và đường cao vào ∆  vuông OCD, ta có:

1 h 2 = 1 O C 2 + 1 O D 2 = 1 1 2 + 1 2 2 = 5 4 ⇒ h = 2 5 5

Vậy khoảng cách từ gốc O tới (d) là  2 5 5 .

a. Em tự giải

b. Từ giả thiết ta có \(A\left(-2;1\right)\) và \(B\left(4;4\right)\)

Gọi phương trình (d) có dạng \(y=ax+b\), do (d) qua A và B nên:

\(\left\{{}\begin{matrix}-2a+b=1\\4a+b=4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b=2\end{matrix}\right.\) \(\Rightarrow y=\dfrac{1}{2}x+2\)

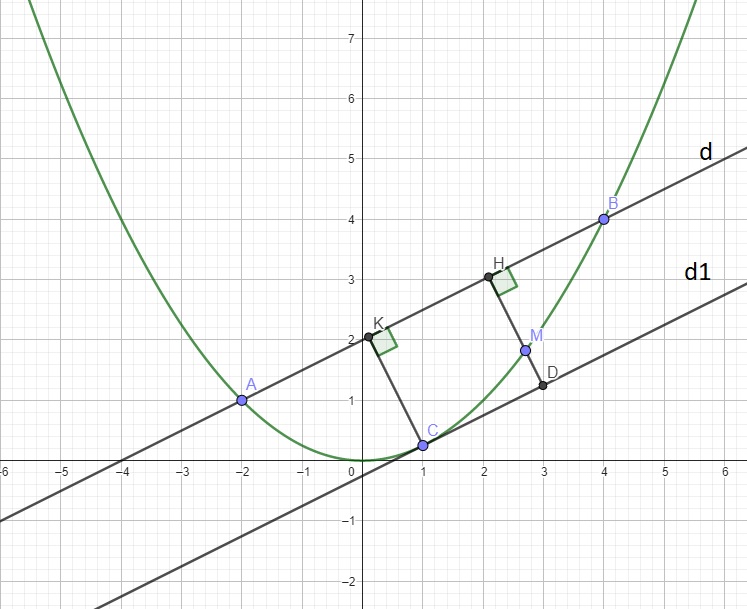
c. Câu này có vài cách giải cho lớp 9, cách nhanh nhất là sử dụng tính chất tiếp tuyến.

Từ M kẻ \(MH\perp AB\Rightarrow S_{ABM}=\dfrac{1}{2}MH.AB\)

Do AB cố định \(\Rightarrow S_{max}\) khi \(MH_{max}\)

Gọi \(d_1\) là đường thẳng song song d và tiếp xúc (P), gọi C là tiếp điểm \(d_1\) và (P)

Do \(d_1\) song song (d) nên pt có dạng: \(y=\dfrac{1}{2}x+b\)

Phương trình hoành độ giao điểm \(d_1\) và (P):

\(\dfrac{1}{4}x^2=\dfrac{1}{2}x+b\Rightarrow x^2-2x-4b=0\) (1)

Do \(d_1\) tiếp xúc (P) \(\Rightarrow\left(1\right)\) có nghiệm kép

\(\Rightarrow\Delta'=1+4b=0\Rightarrow b=-\dfrac{1}{4}\)

Thế vào (1) \(\Rightarrow x_C^2-2x_C+1=0\Rightarrow x_C=1\Rightarrow y_C=\dfrac{1}{4}\) \(\Rightarrow C\left(1;\dfrac{1}{4}\right)\)

Từ C kẻ \(CK\perp d\)

Giả sử HM kéo dài cắt \(d_1\) tại D \(\Rightarrow\) tứ giác CKHD là hình chữ nhật (2 cặp cạnh đối song song và 1 góc vuông)

\(\Rightarrow CK=DH\)

Mà \(DH=MH+MD\ge MH\Rightarrow CK\ge MH\)

\(\Rightarrow MH_{max}=CK\) khi M trùng C

Hay \(M\left(1;\dfrac{1}{4}\right)\)

Câu hỏi của Yến Nhi - Toán lớp 6 | Học trực tuyến

toán lớp 6 thì có liên quan gì đến toán lớp 10

Đường tròn ngoại tiếp tam giác ABC là ảnh của đường tròn (T) qua phép vị tự tâm O tỉ số \(k=2\)

\(\Rightarrow\) Phương trình đường tròn ngoại tiếp tam giác:

\(\left(x-2\right)^2+\left(y+1\right)^2=25\)

(Tọa độ tâm nhân 2 lần và bán kính nhân 2 lần)

ta có pt đường cao kẻ từ B:(d1) x+3y-5=0 
vì AC _|_ (d1) và AC đi qua C(-1; -2) 
=> pt AC: 3(x+1) -(y+2) =0 
<=> 3x -y + 1=0 
ta có A là giao điểm của AC và đg trung tuyến (d2) kẻ từ A 
=> A là nghiệm của hệ: 
{ 5x+y-9=0 
{ 3x -y + 1=0 
<=> 
x=1 ; y=4 
=> A( 1;4) 

Vì B ∈ (d1) => B(5- 3y; y) 
gọi I là trung điểm BC => I ∈ (d2) 
Vì I là trung điểm BC 
=> 
{ 2xI = xB + xC 
{ 2yI = yB + yC 
<=> 
{ xI= (5-3y-1)/2 = (4-3y)/2 
{ yI= (y -2)/2 

Vì I ∈ (d2) 
=> 5(4-3y)/2 + (y -2)/2 -9 =0 
<=> y= 0 
=> B( 5; 0) 
Vậy A( 1;4) và B( 5; 0)

Ta có pt đường cao kẻ từ B: (d1) x+3y-5=0
Vì AC _|_ (d1) và AC đi qua C(-1; -2)
=> pt AC: 3(x+1) -(y+2) =0
<=> 3x -y + 1=0
Ta có A là giao điểm của AC và đường trung tuyến (d2) kẻ từ A
=> A là nghiệm của hệ:
{ 5x+y-9=0
{ 3x -y + 1=0
<=>
x=1 ; y=4
=> A( 1;4)

Vì B ∈ (d1) => B(5- 3y; y)
Gọi I là trung điểm BC => I ∈ (d2)
Vì I là trung điểm BC
=>
{ 2xI = xB + xC
{ 2yI = yB + yC
<=>
{ xI= (5-3y-1)/2 = (4-3y)/2
{ yI= (y -2)/2

Vì I ∈ (d2)
=> 5(4-3y)/2 + (y -2)/2 -9 =0
<=> y= 0
=> B( 5; 0)
Vậy A( 1;4) và B( 5; 0)

a)Hoành độ giao điểm của (P)và (d) là:

        \(\frac{1}{2}x^2=x+4\)

\(\Leftrightarrow x^2=2x+8\)

\(\Leftrightarrow x^2-2x-8=0\)

\(\Leftrightarrow\left(x+2\right).\left(x-4\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}x+2=0\\x-4=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-2\\x=4\end{cases}}}\)

Thay \(x=-2\)vào (d) ta được:

     \(y=-2+4=2\)

Thay \(x=4\)vào (d)ta được:

    \(y=4+4=8\)

Vậy \(A\left(-2;2\right),B\left(4;8\right)\)hoặc \(A\left(4;8\right),B\left(-2;2\right)\)

b)Mk ko bt làm

b) Thay x=-4 vào (P), ta được:

\(y=\dfrac{-1}{4}\cdot\left(-4\right)^2=\dfrac{-1}{4}\cdot16=-4\)

Thay x=2 vào (P), ta được:

\(y=\dfrac{-1}{4}\cdot2^2=\dfrac{-1}{4}\cdot4=-1\)

Vậy: A(-4;-4) và B(2;-1)

Gọi (d): y=ax+b(a\(\ne\)0) là phương trình đường thẳng đi qua hai điểm A và B

\(\Leftrightarrow\left\{{}\begin{matrix}-4a+b=-4\\2a+b=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-6a=-3\\2a+b=-1\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b=-1-2a=-1-2\cdot\dfrac{1}{2}=-1-1=-2\end{matrix}\right.\)

Vậy: (d): \(y=\dfrac{1}{2}x-2\)

cảm ơn nhiều ạ