(- 118) - 93 - 82
Mình cần các bước giải phép tính này ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a,\dfrac{-13}{5}-\dfrac{-7}{15}.\dfrac{120}{63}+\dfrac{4}{5}\\ =\dfrac{-13}{5}+\dfrac{8}{9}+\dfrac{4}{5}\\ =\dfrac{-77}{45}+\dfrac{4}{5}\\ =\dfrac{-41}{45}\\ b.\left(7\dfrac{5}{9}+2\dfrac{2}{3}\right)-5\dfrac{2}{9}\\ =\left(\dfrac{68}{9}+\dfrac{8}{3}\right)-\dfrac{47}{9}\\ =\dfrac{92}{9}-\dfrac{47}{9}\\ =5\)
2)\(-\dfrac{13}{5}--\dfrac{7}{15}.\dfrac{120}{63}+\dfrac{4}{5}\)
\(=-\dfrac{13}{5}+\dfrac{7.15.8}{15.9.7}+\dfrac{4}{5}\)
\(=-\dfrac{13}{5}+\dfrac{8}{9}+\dfrac{4}{5}\)
\(=\left(-\dfrac{13}{5}+\dfrac{4}{5}\right)+\dfrac{8}{9}\)
\(=-\dfrac{9}{5}+\dfrac{8}{9}\)
\(=\dfrac{-81+40}{45}=-\dfrac{41}{45}\)
3)\(\left(7\dfrac{5}{9}+2\dfrac{2}{3}\right)-5\dfrac{2}{9}\)
\(=\left(7\dfrac{5}{9}-5\dfrac{2}{9}\right)+2\dfrac{2}{3}\)
\(=2\dfrac{1}{3}+2\dfrac{2}{3}\)
\(=5\)

\(\text{Δ}=\left(-3\right)^2-4\cdot\left(2m+1\right)\)
=9-8m-4=-8m+5
Để phương trình có nghiệm kép thì -8m+5=0
hay m=5/8
Pt trở thành \(x^2-3x+\dfrac{9}{4}=0\)
hay x=3/2

1) 167 + ( -252 ) + 52 + ( -67 )
= 167 + 52 + ( -252 ) + ( - 67 )
= 219 + - ( 252 + 67 )
= 219 + - ( 319 )
= -100
2) ( -215 ) + ( - 115 ) + ( - 80 )
= - ( 215 + 115 ) + ( - 80 )
= - 330 + ( - 80 )
= - ( 330 - 80 )
= - 250
3) 118 + 107 - ( 118 - 93 )
= 118 + ( 107 - 93 )
= 118 + 14
= 132
4) 1 + 5 + 9 + ..... + 97 + 101
= ( 101 : 1) - 4 = 96
= 101 x 96
= 9696
5) 38 - 138 + 250 - 350
= - 100 + - 100
= 0
6) - ( - 357 ) + ( - 27 ) + ( - 32 )
= - ( - 357 ) + - ( 27 + 32 )
= - ( - 357 ) + - 59
= - ( 357 + 59 )
= - 416
7) 40 + ( 139 - 172 + 99 ) - ( 139 + 199 - 172 )
= 40 + ( 100 - 100 )
= 40 + 0
= 40
8) ( -1 ) + 2 + ( - 3 ) + 4 + ( - 99 ) + 100

số này vô hạn rồi bạn ơi
130,(697674418604651162790) cái trong ( ) là lập đi lập lại
mình tính ra rồi các bạn ko phải tính nữa đâu mình là chủ câu hỏi

1, Hàm số xác định
⇔ cos2x ≠ 4
Mà 0 ≤ cos2x ≤ 1 nên điều trên đúng ∀ x ∈ R
Tập xác định : D = R
2, Hàm số xác định ⇔ \(\left\{{}\begin{matrix}cos3x\ne0\\cosx\ne0\end{matrix}\right.\)
⇔ cos3x ≠ 0
⇔ x ≠ \(\pm\dfrac{\pi}{6}+k.\dfrac{\pi}{3}\) , k ∈ Z
Tập xác định : D = R \ { \(\pm\dfrac{\pi}{6}+k.\dfrac{\pi}{3}\) , k ∈ Z}
3, D = [- 2 ; 2]
4, D = [- 1 ; +\(\infty\)) \ {0 ; 4}
11, sin2x - cos2x ≠ 0
⇔ cos2x ≠ 0

\(99-97+95-93+91-89+...+7-5+3-1\)
\(=\left(99-97\right)+\left(95-93\right)+...\left(7-5\right)+\left(3-1\right)\)
\(=2.25\)
\(=50\)
ta thấy
\(4000:82=48\) ( dư 674)
số \(64>47\Rightarrow\) số bị chia < 4000 là :
\(82.48+47=3983\)
vì 3983<4000 ( t/m)
=> số chia là 48

Câu 20:
Ta có: \(\widehat{A}-\widehat{B}=40^0\Rightarrow\widehat{B}=\widehat{A}-40^0\)
\(\widehat{A}=2\widehat{C}\Rightarrow\widehat{C}=\frac{\widehat{A}}{2}\)
Vì AB//CD (gt) \(\Rightarrow\widehat{A}+\widehat{D}=180^0\)(hai góc trong cùng phía)\(\Rightarrow\widehat{D}=180^0-\widehat{A}\)
Tứ giác ABCD \(\Rightarrow\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\Rightarrow\widehat{A}+\left(\widehat{A}-40^0\right)+\frac{\widehat{A}}{2}+\left(180^0-\widehat{A}\right)=360^0\)
Và đến đây bạn dễ dàng tìm được góc A và từ đó suy ra được góc D.
Câu 29: Ta có:
\(\hept{\begin{cases}xy+x+y=3\\yz+y+z=8\\xz+x+z=15\end{cases}}\Leftrightarrow\hept{\begin{cases}xy+x+y+1=4\\yz+y+z+1=9\\xz+x+z+1=16\end{cases}\Leftrightarrow}\hept{\begin{cases}x\left(y+1\right)+\left(y+1\right)=4\\y\left(z+1\right)+\left(z+1\right)=9\\x\left(z+1\right)+\left(z+1\right)=16\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}\left(x+1\right)\left(y+1\right)=4\\\left(y+1\right)\left(z+1\right)=9\\\left(z+1\right)\left(x+1\right)=16\end{cases}}\)
Đặt \(\hept{\begin{cases}x+1=a\\y+1=b\\z+1=c\end{cases}}\)với a,b,c > 1, khi đó ta có
\(\hept{\begin{cases}ab=4\\bc=9\\ca=16\end{cases}}\Leftrightarrow\hept{\begin{cases}abbc=4.9\\c=\frac{9}{b}\\ca=16\end{cases}}\Leftrightarrow\hept{\begin{cases}16b^2=36\\c=\frac{9}{b}\\a=\frac{16}{c}\end{cases}}\Leftrightarrow\hept{\begin{cases}b^2=\frac{36}{16}=\frac{9}{4}\\c=\frac{9}{b}\\a=\frac{16}{c}\end{cases}}\Leftrightarrow\hept{\begin{cases}b=\frac{3}{2}\\c=\frac{9}{\frac{3}{2}}=6\\a=\frac{16}{6}=\frac{8}{3}\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}x=a-1=\frac{8}{3}-1=\frac{5}{3}\\y=b-1=\frac{3}{2}-1=\frac{1}{2}\\z=c-1=6-1=5\end{cases}}\)
Vậy \(P=x+y+z=\frac{5}{3}+\frac{1}{2}+5=\frac{10+3+30}{6}=\frac{43}{6}\)
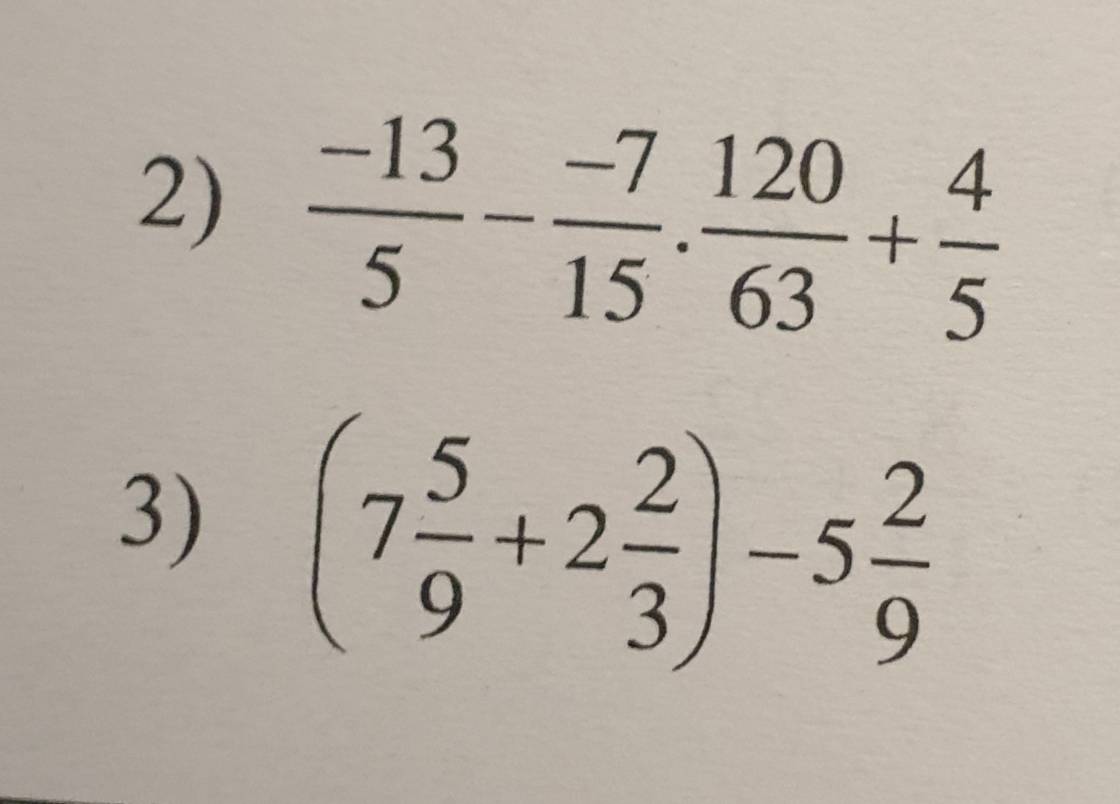 Mình cần giải 2 bài Thực hiện phép tính này ạ
Mình cần giải 2 bài Thực hiện phép tính này ạ


\((- 118) - 93 - 82 = (-118)+(-93)-82 = -(118+93) -82 =(-211)-82=(-211) +( -82)=-293\)
(- 118) - 93 - 82 = (- 118) + (- 93) - 82 = -(118 + 93) - 82 = 211 - 82 = 129