Cho hình chóp S. ABCD có đáy ABCD là hình thang .AD//BC và AD = 2BC .Gọi E và F lần lượt là trung điểm của SA và AD , I là giao điểm của SD và mặt phẳng (BCE). Chứng minh CI // (BEF)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 12 2023
a: Xét (SAD) và (SBC) có
\(S\in\left(SAD\right)\cap\left(SBC\right)\)
AD//BC
Do đó: (SAD) giao (SBC)=xy, xy đi qua S và xy//AD//BC
b: Xét ΔSAB có
M,N lần lượt là trung điểm của AS,AB
=>MN là đường trung bình của ΔSAB
=>MN//SB
Ta có: MN//SB
SB\(\subset\)(SBC)
MN ko nằm trong mp(SBC)
Do đó: MN//(SBC)
CM
4 tháng 10 2019
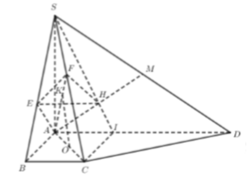
Chọn C.
Phương pháp:
- Chứng minh tứ giác AEFH nội tiếp, từ đó tìm tâm đường tròn ngoại tiếp tam giác EHF .
- Tìm đỉnh hình nón và tính chiều cao, bán kính đáy rồi suy ra thể tích.
Cách giải:
CM
12 tháng 8 2018
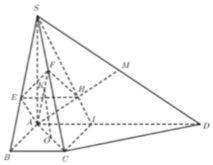
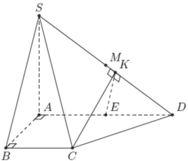
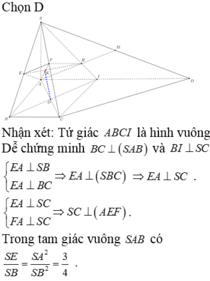
Ta có A E = B C A E / / B C suy ra AECB là hình bình hành. Do A B C ^ = 90 0 nên AECB là hình chữ nhật.
Suy ra C E ⊥ A D mà S A ⊥ C E ⇒ C E ⊥ S A D ⇒ C E ⊥ S D .
Ta lại có E K ⊥ S D ⇒ S D ⊥ E K M ⇒ S D ⊥ C K .
Suy ra góc giữa hai mặt phẳng (SAD) và (SCD) là góc EKC
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 1 2022
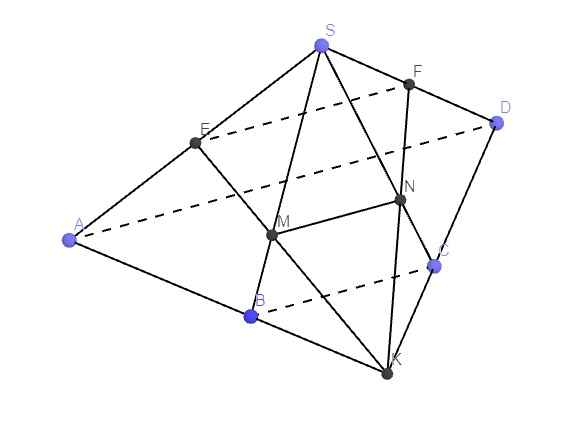
Áp dụng định lý Talet trong tam giác KAD:
\(\dfrac{KB}{KA}=\dfrac{KC}{KD}=\dfrac{BC}{AD}=\dfrac{1}{2}\)
\(\Rightarrow B,C\) lần lượt là trung điểm AK và DK
Mà E, F là trung điểm SA, SD
\(\Rightarrow\) M, N lần lượt là trọng tâm các tam giác SAK và SDK
\(\Rightarrow\dfrac{SM}{SB}=\dfrac{2}{3}\) ; \(\dfrac{SN}{SC}=\dfrac{2}{3}\)
\(\Rightarrow\dfrac{MN}{BC}=\dfrac{SM}{SB}=\dfrac{SN}{SC}=\dfrac{2}{3}\) (Talet)
\(\Rightarrow MN=\dfrac{2}{3}BC=\dfrac{2}{3}.\dfrac{1}{2}AD=\dfrac{1}{3}AD\)
Lại có EF là đường trung bình tam giác SAD \(\Rightarrow EF=\dfrac{1}{2}AD\)
\(\Rightarrow\dfrac{S_{KMN}}{S_{KEF}}=\dfrac{MN}{EF}=\dfrac{\dfrac{1}{3}AD}{\dfrac{1}{2}AD}=\dfrac{2}{3}\)
10 tháng 12 2020
Cho tứ diện ABCD . Gọi G1,G2,G3 lần lượt là trọng tâm của các tam giác ABC,ACD,ABD . Chứng minh mặt phẳng (G1G2G3) // (BCD)
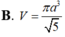
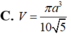
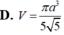
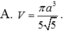
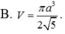
a) Gọi H là trung điểm của SC
Ta có:
DGDH=23(1)DGDH=23(1)
BC∥AD⇒ODOB=OAOC=ADBC=2BC∥AD⇒ODOB=OAOC=ADBC=2
⇒OD=2OB⇒OD=2OB
⇒ODBD=23(2)⇒ODBD=23(2)
Từ (1) và (2) ⇒DGDH=ODBD⇒OG∥BH⇒DGDH=ODBD⇒OG∥BH
BH⊂(SBC)⇒OG∥(SBC)BH⊂(SBC)⇒OG∥(SBC)
b) Gọi M’ là trung điểm của SA⇒MM′∥ADSA⇒MM′∥AD và MM′=AD2MM′=AD2. Mặt khác vì BC∥ADBC∥AD và BC=AD2BC=AD2 nên BC∥MM′BC∥MM′ và BC=MM′BC=MM′.
Do đó tứ giác BCMM’ là hình bình hành ⇒CM∥BM′⇒CM∥BM′ mà BM′⊂(SAB)BM′⊂(SAB)
⇒CM∥(SAB)⇒CM∥(SAB)
c) Ta có: OCOA=12OCOA=12 nên OCCA=13OCCA=13. Mặt khác vì SC=32SISC=32SI nên CICS=13CICS=13.
OCCA=CICS⇒OI∥SAOCCA=CICS⇒OI∥SA
OI⊂(BID)⇒SA∥(BID)