Bài 3. Trong một buổi tập đồng diễn thể dục có khoảng 400 đến 500 người tham gia. Thầy tổng phụ trách cho xếp thành hàng 5, hàng 6 và hàng 8 thì đều thừa một người. Hỏi có chính xác bao nhiêu người dự buổi tập đồng diễn thể dục.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 12 2021
Gọi số người trong buổi tập đồng diễn thể dục là x (người, x ∈ N*, 400 ≤ x ≤ 500)
Vì thầy tổng phụ trách xếp thành hàng 5 thì thừa 1 người nên x chia 5 dư 1 hay (x - 1) ⁝ 5
Vì thầy tổng phụ trách xếp thành hàng 6 thì thừa 1 người nên x chia 6 dư 1 hay (x - 1) ⁝ 6
Vì thầy tổng phụ trách xếp thành hàng 8 thì thừa 1 người nên x chia 8 dư 1 hay (x - 1) ⁝ 8
Do đó (x - 1) là bội chung của 5; 6 và 8.
Ta có: 5 = 5; 6 = 2. 3; 8 = 23
BCNN(5; 6; 8) = 23.3.5 = 120
(x - 1) B(120) = {0; 120; 240; 360; 480; 600;…}
Ta có bảng sau:
x – 1 | 0 | 120 | 240 | 360 | 480 | 600 |
x | 1 | 121 | 241 | 361 | 481 | 601 |
Mà buổi tập đồng diễn thể dục có khoảng 400 đến 500 người tham gia nên
Vì thế x = 481
MH
26 tháng 12 2021
Tham khảo
Gọi số người dự buổi tập đồng diễn thể dục là `x`
Xếp số người đó thành hàng `5,6` và `8` thì thấy thừa một người
`⇒x` chia `5,6,8` dư `1`
`⇒x-1⋮5,6,8`
`⇒x-1∈BC(5;6;8)`
Ta có: `5=5;6=2.3;8=2^3`
`⇒BCN N(5;6;8)=2^3. 3.5=120`
`⇒BC(5;6;8)={0;120;240;360;480;600;…}`
`⇒x∈{1;121;241;361;481;601;…}`
Vì có khoảng `400` đến `500` người tham gia
`⇒400≤x≤500`
`⇒x=481`
Vậy có `481` người dự buổi tập đồng diễn thể dục
29 tháng 10 2021
Gọi số người dự buổi tập đồng diễn thể dục là `x`
Xếp số người đó thành hàng `5,6` và `8` thì thấy thừa một người
`⇒x` chia `5,6,8` dư `1`
`⇒x-1⋮5,6,8`
`⇒x-1∈BC(5;6;8)`
Ta có: `5=5;6=2.3;8=2^3`
`⇒BCN N(5;6;8)=2^3. 3.5=120`
`⇒BC(5;6;8)={0;120;240;360;480;600;…}`
`⇒x∈{1;121;241;361;481;601;…}`
Vì có khoảng `100 người tham gia
x=1
Vậy có1 người dự buổi tập đồng diễn thể dục
Sai mik sorry nha
Hok tốt
PL
11 tháng 11 2023
gọi số học sinh tham gia buổi đồng diễn là x ( x <_ 200 <_ 300)
ta có : phần sau tự làm ik cách này dài lắm
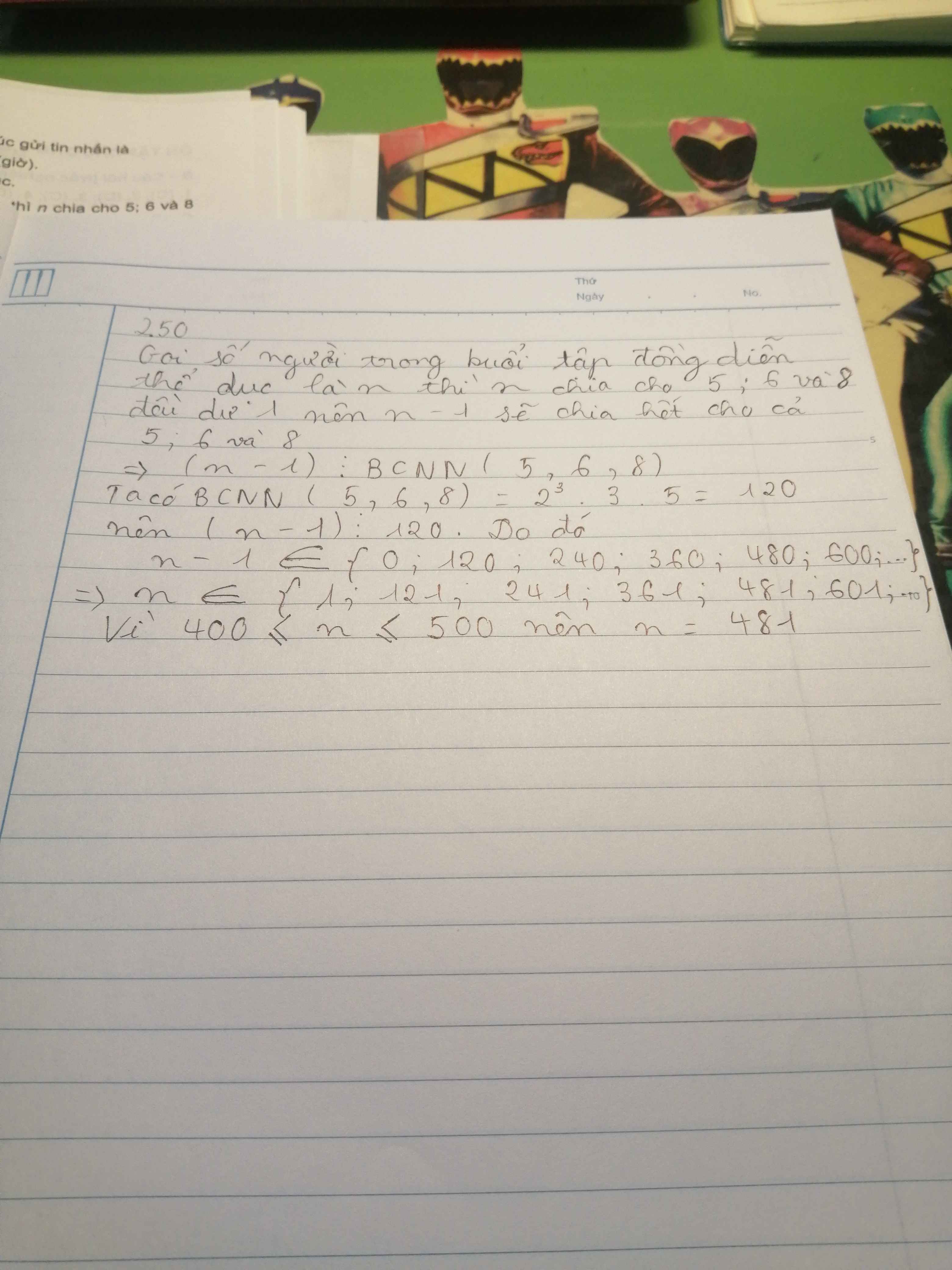
Gọi số người chính xác là x
Theo đề, ta có: \(x-1\in BC\left(5;6;8\right)\)
hay x=481
Gọi số người là \(x(người;x\in \mathbb{N^*})\)
Ta có \(x-1\in BC(5,6,8)=B(120)=\text{{0;120;240;360;480;600;...}}\)
Mà \(400{<}x{<}500\Rightarrow x-1=480\Rightarrow x=481\)
Vậy có 481 người tham dự