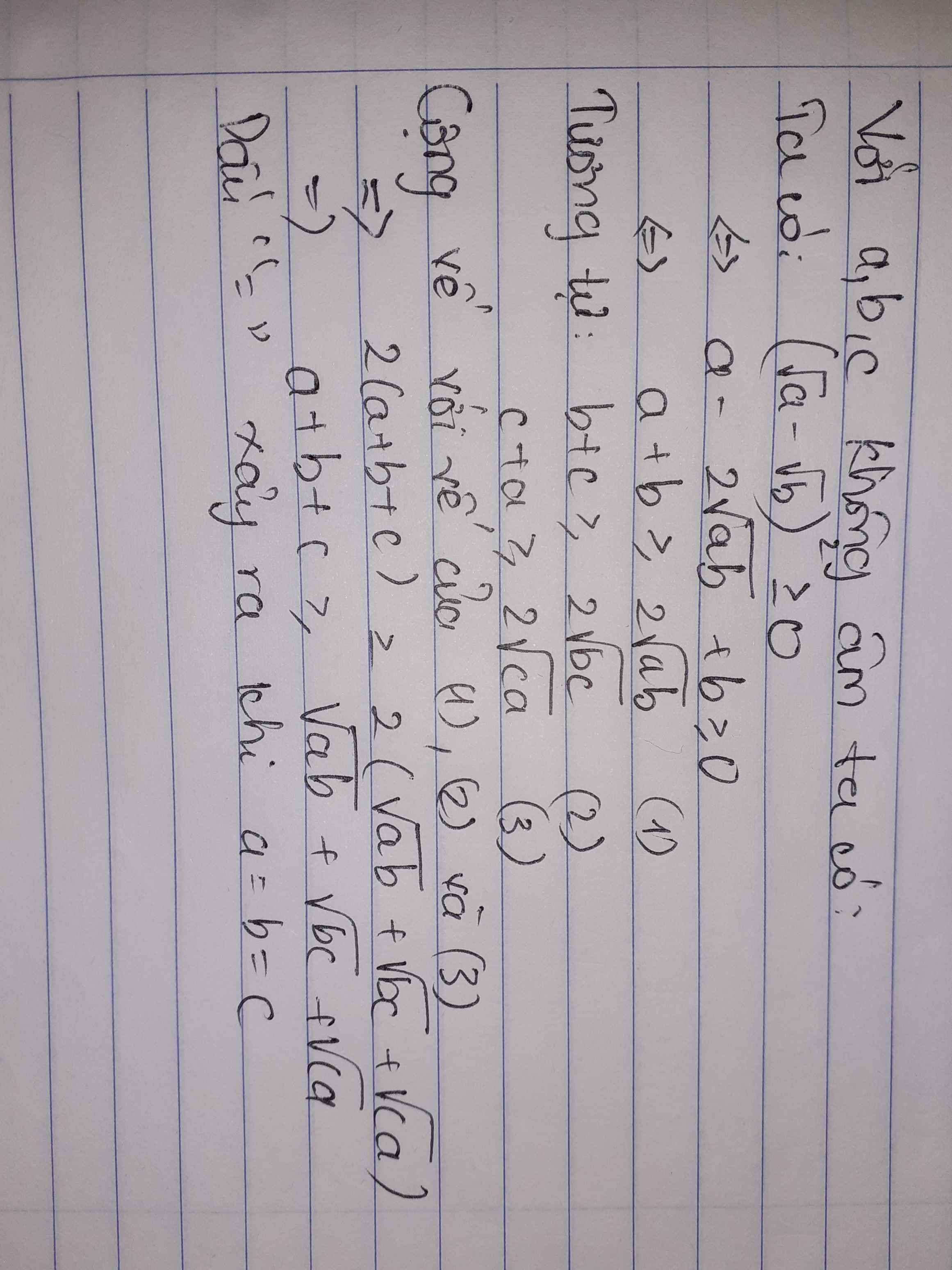a.b-a.c+b.c-c²=-1

a.b-a.c+b.c-c.c=-1

a.(b-c)+c.(b-c)=-1

(b-c).(a+c)=-1

Mà a;b;c\(\in\)Z

=>b-c=-1;a+c=1

 b=-1+c;a=1-c

=>a đối b

Hoặc b-c=1;a+c=-1

b=1+c;a=-1-c

=>a đối b

=>a;b đối nhau khi a.b-a.c+b.c-c²=-1

Chúc bn học tốt

\(ab-ac+bc-c^2=-1\)\(\Leftrightarrow a\left(b-c\right)+c\left(b-c\right)=-1\)

\(\Leftrightarrow\left(a+c\right)\left(b-c\right)=-1=1.\left(-1\right)=\left(-1\right).1\)

mà \(1+\left(-1\right)=0\)\(\Rightarrow\left(a+c\right)+\left(b-c\right)=0\)

\(\Leftrightarrow a+c+b-c=0\)\(\Leftrightarrow a+b=0\)

Vậy a và b là 2 số đối nhau

=> a.(b-c) + c.(b-c)=-1

=> (a+c).(b-c) = -1

Mà a,b,c thuộc Z => a+c và b-c đều thuộc Z => a+c=1;b-c=-1 hoặc a+c=-1;b-c=1

=> a=-b

=> ĐPCM 

k mk nha

bấm vào chữ 0 đúng sẽ hiện ra kết quả 

=>a(b-c)+c(b-c)=-1=>(b-c)(a+c)=1=>b-c=-1.a+c=1 công theo từng vế ta đc a+b=0=> a=-b=> a và b đối nhau

tương tự vs b-c=1;a+c=-1

Đề bạn sai  nhé mk chữa luôn

Điều phải chứng minh tương đương với

\(2a+2b+2c-2\sqrt{ab}-2\sqrt{bc}-2\sqrt{ca}\ge0\\ \Leftrightarrow\left(a+b-2\sqrt{ab}\right)+\left(b+c-2\sqrt{bc}\right)+\left(c+a-2\sqrt{ca}\right)\ge0\\ \Leftrightarrow\left(\sqrt{a}-\sqrt{b}\right)^2+\left(\sqrt{b}-\sqrt{c}\right)^2+\left(\sqrt{c}-\sqrt{a}\right)^2\ge0\)

(luôn đúng với mọi a,b,c không âm)

Dấu = xảy ra khi a=b=c >=0 

Mk làm mẫu câu a nha

a, => xy+3x-7y-21 = 0

=> (xy+3x)-(7y+21) = 0

=> x.(y+3)-7.(y+3) = 0

=> (y+3).(x-7) = 0

=> y+3=0 hoặc x-7=0

=> x=7 hoặc y=-3

Tk mk nha

\(a)\) \(xy+3x-7y=21\)

\(\Leftrightarrow\)\(x\left(y+3\right)-\left(7y+21\right)=0\)

\(\Leftrightarrow\)\(x\left(y+3\right)-7\left(y+3\right)=0\)

\(\Leftrightarrow\)\(\left(x-7\right)\left(y+3\right)=0\)

\(\Leftrightarrow\)\(\orbr{\begin{cases}x-7=0\\y+3=0\end{cases}}\)

\(\Leftrightarrow\)\(\orbr{\begin{cases}x=7\\y=-3\end{cases}}\)

Vậy \(x=7\) và \(y=-3\)

Giải:

Từ giả thiết ta có:

\(\left(1-b\right)\left(1-c\right)\ge0\)

\(\Leftrightarrow1-\left(b+c\right)+bc\ge0\)

\(\Leftrightarrow bc+1\ge b+c\)

\(\Rightarrow\frac{a}{bc+1}\le\frac{a}{b+c}\le\frac{a}{a+b}\left(1\right)\)

Tương tự ta có:

\(\frac{b}{ac+1}\le\frac{b}{a+c}\le\frac{b}{a+b}\left(2\right)\)

\(\frac{c}{ab+1}\le c\le1\left(3\right)\)

Cộng theo vế \(\left(1\right);\left(2\right);\left(3\right)\) ta được:

\(\frac{a}{bc+1}+\frac{b}{ac+1}+\frac{c}{ab+1}\le\frac{a+b}{a+b}+1=2\)

Vậy \(\frac{a}{bc+1}+\frac{b}{ac+1}+\frac{c}{ab+1}\le2\) (Đpcm)