Cho tam giác ABC. Trên tia đối của tia AB lấy điểm D sao cho AD = 2AB. Trên tia đối của tia AC lấy điểm E sao cho AE = 2AC. Chứng minh tam giác ADE đồng dạng với tam giác ABC. Tìm tỉ số đồng dạng.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 4 2020
ta lay Ab chia cho 2000 jsfuigasfugsuiegSUIBBUIHRDUIPOHGSDUFGHUSUHIUSIUGSRG
Q
23 tháng 3 2017
Có: tam giác ABC đồng dạng với tam giác ADE
=>AB/AD=AC/AE
Có AB/AD=AB/2AB=1/2
AC/AE=AC/2AC=1/2
Vậy tam giác ABC đồng dạng với tam giác ADE the tỉ số đồng dạng là 1/2
KV
24 tháng 1
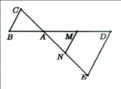
Do 2BD = BA (gt)
⇒ AD = AB + BD
= 2BD + BD
= 3BD
⇒ AB/AD = 2/3 (1)
Do 2CE = CA (gt)
⇒ AE = AC + CE
= 2CE + CE
= 3CE
⇒ AC/AE = 2/3 (2)
Từ (1) và (2) ⇒ AB/AD = AC/AE = 2/3
Xét ∆ABC và ∆ADE có:
AB/AD = AC/AE (cmt)
A chung
⇒ ∆ABC ∽ ∆ADE (c-g-c)
12 tháng 5 2023
1,3: Xet ΔADE và ΔACB có
AD/AC=AE/AC
góc DAE=góc CAB
=>ΔADE đồng dạng vói ΔACB
=>góc ADE=góc ACB
=>DE//BC
2: DE/CB=AD/AC=3/10
15 tháng 2 2019
Có: tam giác ABC đồng dạng với tam giác ADE
=>AB/AD=AC/AE
Có AB/AD=AB/2AB=1/2
AC/AE=AC/2AC=1/2
Vậy tam giác ABC đồng dạng với tam giác ADE the tỉ số đồng dạng là 1/2
Ta có: \(\left\{{}\begin{matrix}\dfrac{AD}{AB}=\dfrac{2AB}{AB}=2\\\dfrac{AE}{AC}=\dfrac{2AC}{AC}=2\end{matrix}\right.\Rightarrow\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
Xét tam giác ADE và tam giác ABC ta có:
\(\dfrac{AD}{AB}=\dfrac{AE}{AC}\left(cmt\right)\)
Góc DAE = Góc BAC (đối đỉnh)
\(\Rightarrow\Delta ADE\sim\Delta ABC\left(c-g-c\right)\)
\(\Rightarrow\dfrac{AD}{AB}=\dfrac{ED}{BC}=\dfrac{AE}{AC}\)