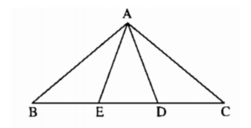
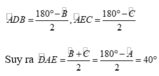Bài 3 tam giác ABC cân tại A có A bằng 100 độ lấy các điểm D và E trên cạnh BC sao cho BD = BA, CE = CA tính số đo góc DAE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NH
Nguyễn Hoàng Minh
26 tháng 12 2021
Đúng(1)
Những câu hỏi liên quan
27 tháng 7 2016
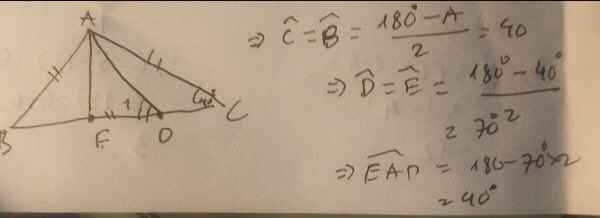
đừng tích ai nhá, tôi về mình giải cho, giờ mik phải đi học thêm
26 tháng 12 2018
ΔABD cân tại B có 
ΔACE cân tại C có 
CM
30 tháng 7 2018
+) Ta có:
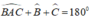(tổng ba góc trong 1 tam giác)
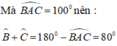
Lại có: tam giác ABC là tam giác cân tại A nên:
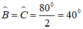
+)Xét tam giác ABD có BA= BD (giả thiết) nên tam giác ABD cân tại B.
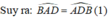
Lại có;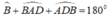 
( tổng ba góc trong 1 tam giác)
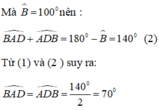
+) Tương tự, ta có tam giác AEC cân tại C ( vì CA =CE)
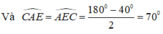
+) Xét tam giác ADE có:
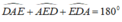( tổng ba góc trong tam giác)
Suy ra:
26 tháng 12 2018
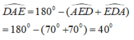
ΔABD cân tại B có
ΔACE cân tại C có
YN
26 tháng 12 2021
Answer:
Ta có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
\(\Rightarrow100^o+\widehat{C}+\widehat{B}=180^o\)
\(\Rightarrow2\widehat{B}=80^o\)
\(\Rightarrow\widehat{B}=\widehat{C}=40^o\)
Ta có: Tam giác ACE cân tại C
Mà: \(\widehat{A}+\widehat{C}+\widehat{E}=180^o\)
\(\Rightarrow2\widehat{E}+40^o=180^o\)
\(\Rightarrow2\widehat{E}=140^o\)
\(\Rightarrow\widehat{E}=70^o\) (1)
Ta có: Tam giác ABD cân tại B
Mà: \(\widehat{A}+\widehat{B}+\widehat{D}=180^o\)
\(\Rightarrow2\widehat{D}+40^o=180^o\)
\(\Rightarrow2\widehat{D}=140^o\)
\(\Rightarrow\widehat{D}=70^o\) (2)
Từ (1) và (2) \(\Rightarrow\widehat{A}+\widehat{E}+\widehat{D}=180^o\)
\(\Rightarrow\widehat{A}+2.70^o=180^o\)
\(\Rightarrow\widehat{A}+140^o=180^o\)
\(\Rightarrow\widehat{A}=40^o\)
Vậy \(\widehat{DAE}=40^o\)
KH
19 tháng 5 2017
Ta có: \(\Delta\)ABC cân tại A
\(\widehat{A}\) = 100o
=> \(\widehat{B}\) = \(\widehat{C}\) = 20o (Vì tổng các góc trong 1 \(\Delta\) luôn bằng 180o)
* Vì: BA = BD (gt)
=> \(\Delta\)BAD cân tại B.
Ta có: \(\widehat{BAD}+\widehat{B}+B\widehat{DA}=180^O\)
\(\widehat{BAD}+40^{O^{ }}+\widehat{BD}A=180^O\)
\(B\widehat{AD}+\widehat{BDA}=180^{O^{ }}-40^O=120^O\)
Mà \(\Delta\)ABD cân
=> \(\widehat{A}\)= \(\widehat{BDA}\) = 70o
* Vì AC = CE (gt)
=> \(\Delta\)ACE cân tại C.
Ta có: \(\widehat{EAC}+\widehat{C}+\widehat{CEA}=180^O\)
\(\widehat{EAC}+40^O+\widehat{CEA}=180^O\)
\(\widehat{EAC}+\widehat{CEA}=180^O-40^O=140^O\)
Mà \(\Delta\)ACE cân
=> \(\widehat{EAC}=\widehat{CEA}=70^O\)
* Xét \(\Delta\)AED có: \(\widehat{AED}=\widehat{ADE}=70^O\)
Áp dụng định lý tổng các góc trong 1 \(\Delta\) bằng 180o, ta có:
\(\widehat{DAE}+\widehat{ADE}+\widehat{DEA}=180^O\)
\(\widehat{DAE}+70^O+70^O=180^O\)
\(\widehat{DAE}=180^O-70^{O^{ }}-70^O\)
\(\widehat{DAE}=40^O\)
2 tháng 1 2018
mk tg \(\widehat{B}=\widehat{C}=40\) độ tại 180-100=80 và 80:2=40 ms phải Evil Yasuda