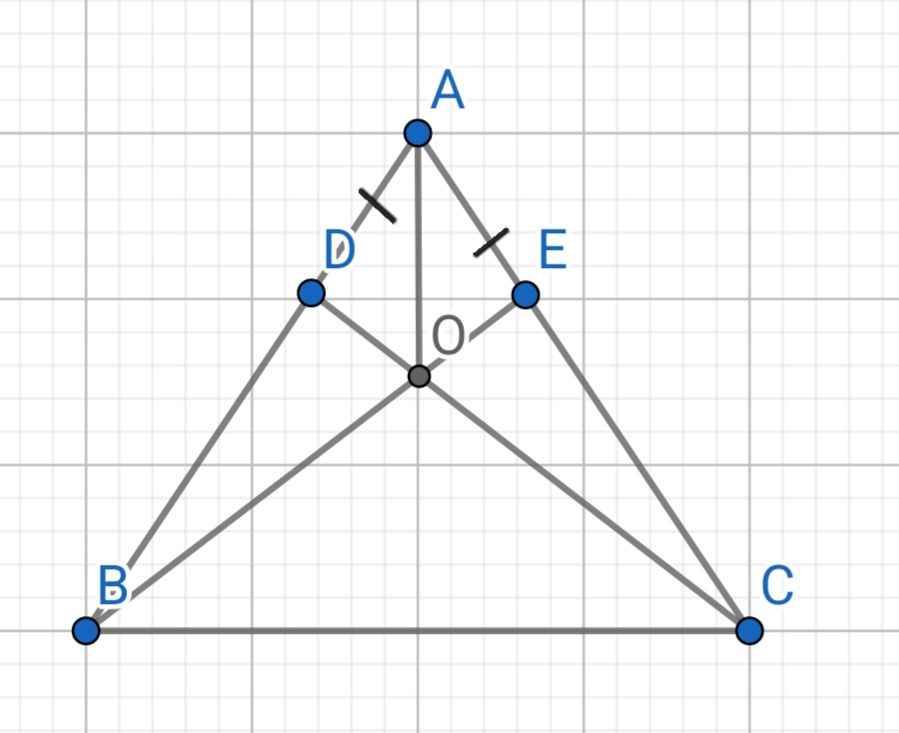
Cho tam giác ABC có AB = AC. Lấy điểm D trên cạnh AB, điểm E trên cạnh AC sao cho AD = AE a) Chứng minh rằng BE = CD b) Gọi O là giao điểm của BE và CD, chứng minh ao là tia phân giác của góc bac
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Cm: a) Xét t/giác ABE và t/giác ACD
có: AB = AC (gt)
\(\widehat{A}\) :chung
AE = AD (gt)
=> t/giác ABE = t/giác ACD (c.g.c)
=> BE = CD (2 cạnh t/ứng)
b)Ta có: AD + DB = AB
AE + EC = AC
mà AD = AE (gt) ; AB = AC (gt)
=> BD = EC
Ta lại có: \(\widehat{ADC}+\widehat{CDB}=180^0\) (kề bù)
\(\widehat{AEB}+\widehat{BEC}=180^0\)(kề bù)
mà \(\widehat{ADC}=\widehat{AEB}\)(vì t/giác ABE = t/giác ACD)
=> \(\widehat{BDC}=\widehat{BEC}\)
Xét t/giác BOD và t/giác COE
có: \(\widehat{DBO}=\widehat{OCE}\) (vì t/giác ABE = t/giác ACD)
BD = EC (cmt)
\(\widehat{BDO}=\widehat{OEC}\) (cmt)
=> t/giác BOD = t/giác COE (g.c.g)
c) Xét t/giác ABO và t/giác ACO
có: AB = AC (gT)
OB = OC (vì t/giác BOD = t/giác COE)
AO : chung
=> t/giác ABO = t/giác ACO (c.c.c)
=> \(\widehat{BAO}=\widehat{CAO}\) (2 góc t/ứng)
=> AO là tia p/giác của \(\widehat{A}\)
d) Xét t/giác ABH và t/giác ACH
có: AB = AC (gt)
\(\widehat{BAH}=\widehat{CAH}\)(cmt)
AH : chung
=> t/giác ABH = t/giác ACH (c.g.c)
=> \(\widehat{BHA}=\widehat{CHA}\) (2 góc t/ứng)
Mà \(\widehat{BHA}+\widehat{CHA}=180^0\) (kề bù)
=> \(\widehat{BHA}=\widehat{CHA}=90^0\) => AH \(\perp\)BC (Đpcm)

a) ta có : AB=AC
Suy ra tam giac ABC cân
Xét tam giac ABE và tam giác ADE ta có
AB=AC(gt)
góc B=gócC(tính chất tam giác cân)
AD=AE(gt)
Suy ra tam giác ABE=tam giac ACD( c.g.c)
Suy ra BE=CD( hai cạnh tương ứng )
b) Ta có O nằm trên cạnh DC và BE
Suy ra DO=EO( DC=BE)
XÉT tam giác ADO và tam giác AEO ta có
AD=AE(gt)
AOchung
DO=EO( chứng minh trên)
Suy ra tam giác AOD = tam giác AEO(c.c.c)
Suy ra góc A1=A2 ( 2 góc tương ứng)
Suy ra AOlà tia phân giác của góc A

a.Xét tam giác DBC và tam giác ECB có:
DB=EC (AB=AC và AD=AE)
góc ABC = góc ACB (cân tại A)
BC là cạnh chung
Do đó tam giác DBC = tam giác ECB (c.g.c)
Suy ra BE= CD (ĐPCM)

 ∆ABC có:
∆ABC có:
AB = AC (gt)
⇒ ∆ABC cân tại A
⇒ ∠ABC = ∠ACB
⇒ ∠DBC = ∠ECB
Do AB = AC (gt)
AD = AE (gt)
⇒ BD = AB - AD = AC - AE = CE
Xét ∆DBC và ∆ECB có:
DB = EC (cmt)
∠DBC = ∠ECB (cmt)
BC là cạnh chung
⇒ ∆DBC = ∆ECB (c-g-c)
⇒ ∠BDC = ∠CEB (hai góc tương ứng)
⇒ ∠BDO = ∠CEO
Do ∆DBC = ∆ECB (cmt)
⇒ ∠BCD = ∠CBE (hai góc tương ứng)
Mà ∠ACB = ∠ABC (cmt)
⇒ ∠ECO = ∠ACB - ∠BCD
= ∠ABC - ∠CBE
= ∠DBO
Xét ∆BOD và ∆COE có:
∠DBO = ∠ECO (cmt)
BD = CE (cmt)
∠BDO = ∠CEO (cmt)
⇒ ∆BOD = ∆COE (g-c-g)
⇒ OD = OE (hai cạnh tương ứng)
Xét ∆ADO và ∆AEO có:
AD = AE (gt)
AO là cạnh chung
OD = OE (cmt)
∆ADO = ∆AEO (c-c-c)
⇒ ∠DAO = ∠EAO (hai góc tương ứng)
⇒ AO là tia phân giác của ∠DAE
Hay AO là tia phân giác của ∠BAC

a: Xét ΔABE và ΔACD có
AB=AC
\(\widehat{A}\) chung
AE=AD
Do đó: ΔABE=ΔACD
Suy ra: BE=CD

a/ Xét tam giác ABE và tam giác ADC có:
Góc A chung
AD=AE(gt)
AB=AC(gt)
=>Tam giác ABE=Tam giác ADC (c.g.c)
->BE=CD( 2 cạnh tương ứng)
b/Ta có:Tam giác ABC có AB=AC-> tam giác ABC cân tại A
Tam giác ABE=tam giác ADC (cmt)
-> Góc DBM= góc ECM (2 góc tương ứng) (1)
mà góc B=góc C ( tam giác ABC cân tại A)
-> Góc MBC=góc MCB
-> Tam giác MBC cân tại M
-> BM=CM(tính chất) (2)
Lại có: AB=AC; AD=AE
=> BD=EC (3)
Từ (1); (2) và (3) suy ra: tam giác BMD=tam giác CME(c.g.c)
c/Xét tam giác ABM và tam giác ACM có:
AB=AC(gt)
Góc ABM= góc ACM(CMt)
BM=CM(cmt)
=> Tam giác ABM=Tam giác ACK (c.g.c)
-> góc BAM=góc CAM(2 góc tương ứng)
hay AM là phân giác góc BAC
a, Xét tam giác ABE và tam giác ACD có
^A _ chung ; AB = AC ; AE = AD
Vậy tam giác ABE = tam giác ACD (c.g.c)
=> BD = CD ( 2 cạnh tương ứng )
b, Xét tam giác BMD và tam giác CME
BD = CE ; ^BMD = ^CME ( đối đỉnh ) ; BD = CE
do AB = AC và AD = AE
Vậy tam giác BMD = tam giác CME (c.g.c)
a: Xét ΔABE và ΔACD có
AB=AC
\(\stackrel\frown{A}\) chung
AE=AD
Do đó: ΔABE=ΔACD
Suy ra: BE=CD