Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
1
a) ta có A đối xứng với F qua O => O là trung điểm của AF
=> BO là trung tuyến của AF (1)
=> CO là trung tuyến của AF (2)
ta lại có O là giao điểm của 3 đường trung trực của tam giác ABC
=> OA = OB =OC (3)
từ 1-2-3 => Góc ABF = góc ACF = 90
=> AB vuông góc với FB
AC vuông góc với FC
mà CH vuông góc AB => CH // BF
BH vuông góc với AC => BH//CF
Xét tứ giác BHCF có
CH // BF
BH//CF
=> HBFC là hình bình hành (dhnb) có HF và BC là 2 đường chéo
M là trung điểm của BC
=> M là trung điểm của HF => 3 điểm H,M,F thẳng hàng ; HM =FM
=> H đối xứng với F qua M
b) Xét tam giác AHF có M là trung điểm của HF O là trung điểm AF
=> OM là đường trung bình
=> OM =1/2AH <=> AH/OM=2
vì H là giao điểm của 2 đường cao BD và CE nên H là trực tâm => AH vuông góc BC
ta lại có OM vuông góc với BC ( M là trung điểm của BC ; O là giao 3 đường trung tuyến => OM là đường trung tuyến của BC )
=> OM // AH => góc HAG =góc GMO (2 góc so le trong)
xét tam giác AHG và tam giác MOG
có :góc HGA =góc MGO (2 góc đối đỉnh)
góc HAG =góc GMO (cmt)
=> đồng dạng (gg) => AH /OM = AG/MG =2
<=> AG=2MG <=> AM = AG + MG =3MG
<=> AG/AM =2/3 mà AM là tiếp tuyến của BC ( m là trnug điểm BC)
=> G là trọng tâm của tma giác ABC
a,Chứng minh được BFCH là hình bình hành
b, Sử dụng kết quả câu a), suy ra HF đi qua M
c, Chú ý: OM là đường trung bình của ∆AHF => ĐPCM
a, BHCK có I là trung điểm hai đường chéo
b, Ta có ∆ABK, ∆ACK vuông tại B và C nên A,B,K,C nằm trên đường tròn đường kính AK
c, Ta có OI là đường trung bình của ∆AHK => OI//AH
d, Gọi AH cắt BC tại M. Ta có BE.BA = BM.BC và CA.CD = CM.BC => ĐPCM
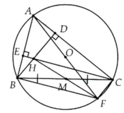
kẻ đường kính AM của (O).
ta có: HC//BM( cùng vuông góc AB), HB//CM( cùng vuông góc AC)
=>HCMB là hình bình hành=>I là trung điểm Bc\C đồng thời là trung điểm MH=>M trùng A=>AA' là đường kính(O)
Xét tam giác AHA' có OI là đường trung bình tam giác => AH=2OI
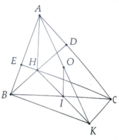
tứ giác ADHE có AEH+ADH=180 => ADHE nội tiếp đường tròn
gọi Q là tâm đường tròn ngoại tiếp tứ giác ADHE
=>EAQ=AEQ
mà EAQ=EDH( cùng chắn EH)=>E\AEQ=EDH(1)
lại có: tứ giác BCDE có D và E cùng nhìn BC dưới 1 góc bằng nhau=>BCDE nội tiếp
=>EDH=ECB(2)
mặt khác: tam giác BEC vuông tại E có EI là trung tuyến ứng với cạnh huyền
=> EI=IC=>tam giav EIC cân
=>ECH=CEI(3)
từ (1), (2) và(3)=>AEQ=CEI
ta có: AEQ+QEC=90=>CEI+QEC=90=>QEI=90=> EI là tiếp tuyến (Q)