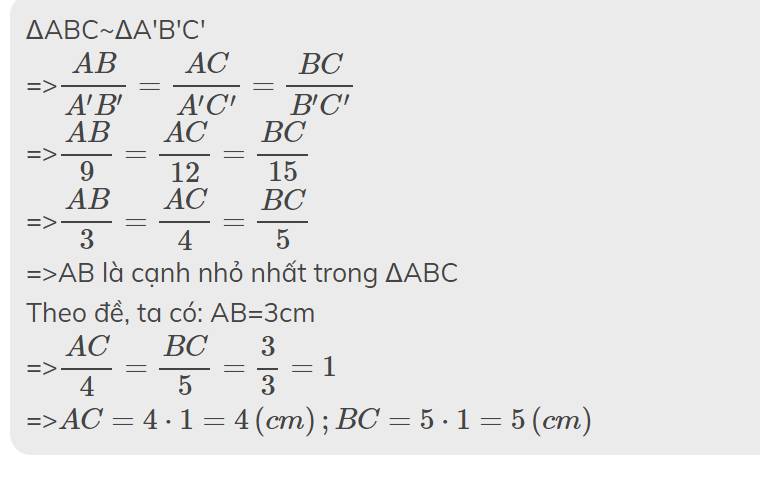Bài 39:Cho tam giác ABC có A',B',C' lần lượt là trung điểm của BC,AC,AB và G là trọng tâm tam giác đó.Gọi M,N,P lần lượt là trung điểm của AG,BG,CG.Chứng minh:
a)Tam giác ABC và A'B'C' đồng dạng.
b)Tam giác MNP đồng dạng với tam giác A'B'C'.Tìm tỉ số đồng dạng(bằng 2 cách khác nhau).