Giúp em với
Em chưa học tứ giác nội tiếp ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét tứ giác ABOC có
\(\widehat{ABO}+\widehat{ACO}=180^0\)
Do đó: ABOC là tứ giác nội tiếp


a)Xét ΔABC cân tại A có AE là trung tuyến
⇒ AE cũng là đường cao của ΔABC
⇒ AE⊥BC \(\Rightarrow\widehat{AEB}=\widehat{AEC}=90^o\)
Xét tứ giác ADBE có \(\widehat{ADB}\) và \(\widehat{AEB}\) cùng nhìn AB dưới góc 90o
⇒ ADBE là tứ giác nội tiếp
⇒ 4 điểm A,D,B,E cùng thuộc (O)
b) Vì BD⊥AC hay HD⊥AC ⇒ ΔHDC vuông tại D
⇒ Tâm của đường tròn đi qua 3 điểm H,D,C là trung điểm của HC
hay I là trung điểm của HC
c) Xét tứ giác HDCE có 2 góc đối \(\widehat{HDC}+\widehat{HEC}=90^o+90^o=180^o\)
⇒ HDCE là tứ giác nội tiếp
⇒ 2 điểm H,E thuộc (I)
Mà 2 điểm H,E cũng thuộc (O)
⇒ Đường tròn tâm O và đường tròn tâm I có 2 điểm chung
a: Ta có: ΔABC cân tại A
mà AE là đường trung tuyến ứng với cạnh đáy BC
nên AE là đường cao ứng với cạnh BC
Xét tứ giác ADEB có
\(\widehat{ADB}=\widehat{AEB}=90^0\)
Do đó: ADEB là tứ giác nội tiếp
hay A,D,E,B cùng thuộc 1 đường tròn

a, ABDC nội tiếp
=> ˆBAH = ˆBCD
ACED nội tiếp
=> OAC^ = CDE^
Lại có ΔDEA nội tiếp đường tròn đường kínhAE
=> DE ⊥ AD
mà AD ⊥ BC
=> DE // BC=>BCD^ =CDE^ ( so le trong)
=>BAH^ = OAC^
b, DE // BC=> BDEC là hình thang (*)
Lại có:
DBC^ = DAC^ ( BDAC nội tiếp) (1)
BCE^= EAB^ ( ABEC nội tiếp) (2)
Lại có: BAH^ = OAC^
=> BAH^ + HAO^ = OAC^ + ˆHAO
=> EAB^ = DAC^ (3)
Từ (1) (2) (3) => DBC^= BCE^ (**)
từ (*) và (**) => BCED là hình thang cân


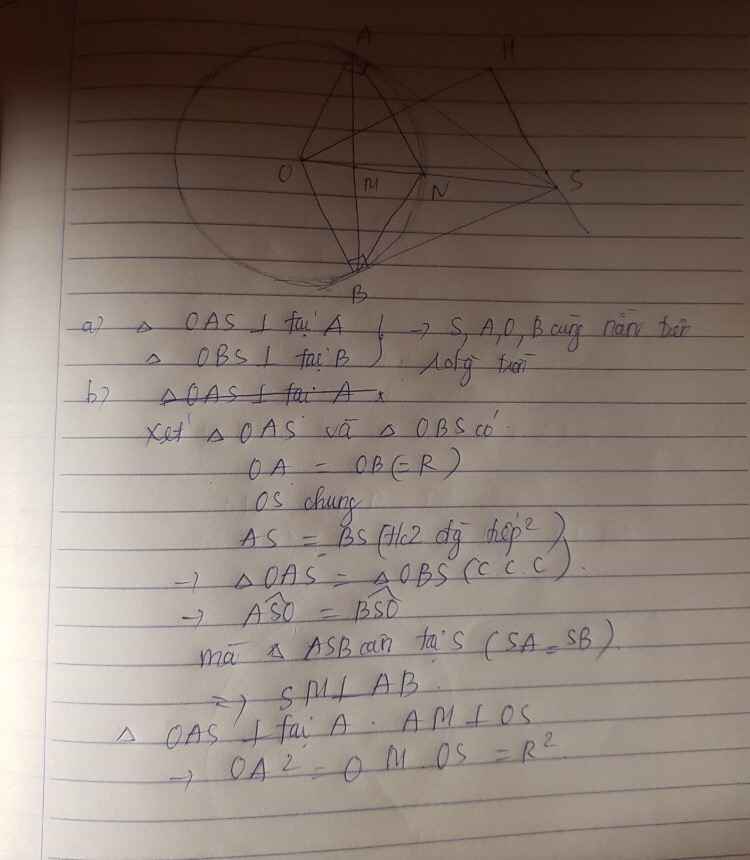


a: Xét tứ giác ABOC có
\(\widehat{ABO}+\widehat{ACO}=180^0\)
Do đó: ABOC là tứ giác nội tiếp