Bài 6 :

Tự vẽ hình nhá :)

a) Gọi O là giao điểm của AC và EF

Xét tam giác ADC có :

EO // DC => AE/AD = AO/AC (1)

Xét tam giác ABC có :

OF // DC

=> CF/CB = CO/CA (2)

Từ (1) và (2) => AE/AD + CF/CB = AO/AC + CO/CA = AO + CO/AC = AC/AC = 1 => đpcm

Bài 7 :

a) Do EF // AB => CF / CA = EF / AB => CF / EF = AC / AB (1)

Dựng MG // AC và M là trung điểm của cạnh BC => GM là đường trung bình của tam giác ABC => G là trung điểm của cạnh AB =>AG = BG

Do DK // GM => AD / AG = DK / GM => AD / BG = DK / GM 

=> DK / AD = GM / BG = \(\frac{\frac{AC}{2}}{\frac{AB}{2}}=\frac{AC}{AB} \left(2\right)\)

Từ (1) và (2) => CF / EF = DK / AD

Mà tứ giác ADEF là hình bình hành ( vì EF // AD và DE // AF ) nên AD = È

=> CF = DK ( đpcm )

Bài 8 : 

Ta có : AB = AM + MB = 11 + 8 = 19 ( cm )

Áp dụng hệ quả định lí Ta-lét vào tam giác ABC, ta có :

AM / AB = AN / AC => AM + AB / AB = AN + AC / AC => 19 + 11 / 19 = AN + 38 / 38 => 30/19 = 38 + AN / 38

=> 1140 = 19.AN + 722

=> AN = ( 1140 - 722 ) / 19 = 22 ( cm )

=> NC = 38 - 12 = 26 ( cm )

chắc sang năm mới làm xong mất 

Xét ΔODE và ΔOCB có

góc ODE=góc OCB

góc DOE=góc COB

=>ΔODE đồng dạng với ΔOCB

=>OD/OC=OE/OB

=>OD*OB=OC*OE

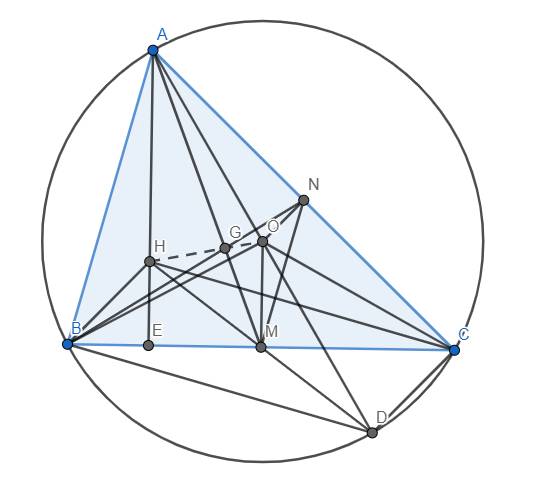
a) Ta chứng minh \(\Delta HAB~\Delta OMN\). Thật vậy, từ đề bài, dễ thấy H, O lần lượt là trực tâm và tâm đường tròn ngoại tiếp của tam giác ABC. Vẽ đường tròn ngoại tiếp này. Dựng đường kính AD của (O). AH cắt BC tại E.

 Ta thấy \(\widehat{ACD}=\widehat{AEB}\left(=90^o\right)\) và \(\widehat{ADC}=\widehat{ABE}\) (góc nội tiếp cùng chắn \(\stackrel\frown{AC}\)). \(\Rightarrow\Delta ACD~\Delta AEB\left(g.g\right)\) \(\Rightarrow\widehat{BAH}=\widehat{CAO}\)

 Mà \(\widehat{CAO}=\widehat{OCA}\), thêm vào đó tứ giác OMCN nội tiếp (vì \(\widehat{OMC}=\widehat{ONC}=90^o\)) nên \(\widehat{OMN}=\widehat{OCN}\). Do đó \(\widehat{HAB}=\widehat{OMN}\)

 Hoàn toàn tương tự, ta suy ra \(\widehat{HBA}=\widehat{ONM}\). Từ đó suy ra \(\Delta HAB~\Delta OMN\left(g.g\right)\) (đpcm)

b) Ta thấy BH//CD\(\left(\perp AC\right)\) và CH//BD\(\left(\perp AB\right)\) nên tứ giác BDCH là hình bình hành. Mà M là trung điểm BC nên M cũng là trung điểm của DH. Lại có O là trung điểm của AD nên OM là đường trung bình của tam giác DHA \(\Rightarrow\left\{{}\begin{matrix}OM//AH\\OM=\dfrac{1}{2}AH\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\widehat{HAG}=\widehat{GMO}\\\dfrac{AH}{OM}=\dfrac{GA}{GM}\left(=2\right)\end{matrix}\right.\)

\(\Rightarrow\Delta AHG~\Delta MOG\left(c.g.c\right)\) (đpcm)

c) Từ \(\Delta AHG~\Delta MOG\Rightarrow\widehat{AGH}=\widehat{MGO}\)

Do A, G, M thẳng hàng nên \(\widehat{AGH}+\widehat{HGM}=180^o\) 

Từ đó suy ra \(\widehat{HGM}+\widehat{MGO}=180^o\) \(\Rightarrow\) H, O, G thẳng hàng.

a, vì BD song song với AC nên góc B2 bằng góc C2. tương tự được góc C1 bằng góc B1.Do đó tam giác ABC = tam giác BAE(g.c.g) (dpcm)

b, vì AC song song với BD nên góc D bằng góc ACF.

vì AF song song với BC nên góc C1= góc CAF = B2.

theo câu a, tam giác ABC= tam giác DCB nên AC=BD, AB=DC

Do đó tam giác BDC=tam giác ACF(g.c.g) nên DC = CF=AB nên DF= DC+CF=2.AB.

Tương tự ta đc; DE=2.AC, EF=2.BC

Do đó Chu vi tam giác DEF bằng 2 lần chu vi tam giác ABC và bằng 30 cm

Hay quá!!!!!!!!!!

a: Xét ΔODA và ΔOKM  có

\(\widehat{ODA}=\widehat{OKM}\)(hai góc so le trong, AD//KM)

\(\widehat{DOA}=\widehat{KOM}\)

Do đó: ΔODA đồng dạng với ΔOKM

=>\(\dfrac{OD}{OK}=\dfrac{OA}{OM}\)

=>\(OD\cdot OM=OA\cdot OK\)

b: Xét ΔABC có AD là phân giác

nên \(\dfrac{DB}{AB}=\dfrac{DC}{AC}\)

=>\(\dfrac{DB}{5}=\dfrac{DC}{10}\)

=>\(\dfrac{DB}{1}=\dfrac{DC}{2}\)

mà DB+DC=BC=12cm

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{DB}{1}=\dfrac{DC}{2}=\dfrac{DB+DC}{1+2}=\dfrac{12}{3}=4\)

=>\(DB=4\cdot1=4cm;DC=4\cdot2=8cm\)

c: Ta có: EM//CA

=>\(\widehat{AEK}=\widehat{KAD}=\widehat{CAD}\left(1\right)\)

Ta có: EK//AD

=>\(\widehat{EKA}=\widehat{BAD}\)(hai góc đồng vị)(2)

ta có:AD là phân giác của góc BAC

=>\(\widehat{BAD}=\widehat{CAD}\left(3\right)\)

Từ (1),(2),(3) suy ra \(\widehat{AEK}=\widehat{AKE}\)

=>ΔAEK cân tại A

=>AK=AE

Tứ giác `DACM` có: 

`DA` // `MC`

`DM` // `AC`

`=>` Tứ giác `DACM` là hình bình hành

`=> hat{D} = hat{C}; DA = MC`

Tương tự: 

Tứ giác `AEMB` là hình bình hành có `hat{B} = hat{E}; AE = BM`

Ta có: 

* `DE = DA + AE`

* `BC = BM + MC`

mà `DA = MC; AE = BM`

`=> DE = MC`

Xét tam giác `MDE` và tam giác `ACB` có: 

`hat{B} = hat{E}`

` DE = MC`

`hat{D} = hat{C}`

`=>` tam giác `MDE =` tam giác `ACB` (góc - cạnh - góc)