Bài 4: Cho đường tròn (O) và một điểm A nằm ngoài đường tròn. Từ A vẽ hai tiếp tuyến AB, AC của đường tròn (O) (B và C là hai tiếp điểm). Vẽ đường kính BD của đường tròn (O) a) Chứng minh: OA BC và DC // OA. b) Đường thẳng AD cắt (O) tại điểm thứ hai là E. Chứng minh: AE.AD = AC2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét (O) có
AB,AC là tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
=>OA\(\perp\)BC tại trung điểm của BC
=>OA\(\perp\)BC tại H và H là trung điểm của BC
b: Xét (O) có
ΔBED nội tiếp
BD là đường kính
Do đó: ΔBED vuông tại E
=>BE\(\perp\)ED tại E
=>BE\(\perp\)AD tại E
Xét ΔDBA vuông tại B có BE là đường cao
nên \(AE\cdot AD=AB^2\left(3\right)\)
Xét ΔOBA vuông tại B có BH là đường cao
nên \(AH\cdot AO=AB^2\left(4\right)\) và \(OH\cdot OA=OB^2\)
Từ (3) và (4) suy ra \(AE\cdot AD=AH\cdot AO\)
c: Xét ΔOKH vuông tại K và ΔOIA vuông tại I có
\(\widehat{KOH}\) chung
Do đó: ΔOKH đồng dạng với ΔOAI
=>\(\dfrac{OK}{OA}=\dfrac{OH}{OI}\)
=>\(OK\cdot OI=OH\cdot OA\)
mà \(OH\cdot OA=OB^2\)
nên \(OK\cdot OI=OB^2=R^2=OD^2\)
=>\(\dfrac{OK}{OD}=\dfrac{OD}{OI}\)
Xét ΔOKD và ΔODI có
\(\dfrac{OK}{OD}=\dfrac{OD}{OI}\)
\(\widehat{KOD}\) chung
Do đó: ΔOKD đồng dạng với ΔODI
=>\(\widehat{ODK}=\widehat{OID}=90^0\)
=>KD là tiếp tuyến của (O)

a: Xét tứ giác ABOC có
\(\widehat{ABO}+\widehat{ACO}=180^0\)
Do đó: ABOC là tứ giác nội tiếp

a: Xét tứ giác ABOC có \(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)
nên ABOC là tứ giác nội tiếp
=>A,B,O,C cùng nằm trên 1 đường tròn
b: Xét (O) có
AB,AC là các tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA là trung trực của BC
=>OA\(\perp\)BC tại H và H là trung điểm của BC
Xét (O) có
ΔBED nội tiếp
BD là đường kính
Do đó: ΔBED vuông tại E
=>BE\(\perp\)ED tại E
=>BE\(\perp\)AD tại E
Xét ΔABD vuông tại B có BE là đường cao
nên \(AE\cdot AD=AB^2\)(3)
=>\(AE\cdot AD=AC^2\)
Xét ΔABO vuông tại B có BH là đường cao
nên \(AH\cdot AO=AB^2\left(4\right)\)
Từ (3) và (4) suy ra \(AE\cdot AD=AH\cdot AO\)
=>\(\dfrac{AE}{AO}=\dfrac{AH}{AD}\)
Xét ΔAEH và ΔAOD có
\(\dfrac{AE}{AO}=\dfrac{AH}{AD}\)
góc EAH chung
Do đó: ΔAEH đồng dạng với ΔAOD
=>\(\widehat{AHE}=\widehat{ADO}\)
c: Ta có: ΔOED cân tại O
mà OK là đường trung tuyến
nên OK\(\perp\)ED tại K
Xét ΔBOA vuông tại B có BH là đường cao
nên \(OH\cdot OA=OB^2=R^2\)
Xét ΔOKA vuông tại K và ΔOHF vuông tại H có
\(\widehat{KOA}\) chung
Do đó: ΔOKA đồng dạng với ΔOHF
=>\(\dfrac{OK}{OH}=\dfrac{OA}{OF}\)
=>\(OK\cdot OF=OA\cdot OH\)
=>\(OK\cdot OF=R^2=OD^2\)
=>\(\dfrac{OK}{OD}=\dfrac{OD}{OF}\)
Xét ΔOKD và ΔODF có
\(\dfrac{OK}{OD}=\dfrac{OD}{OF}\)
góc KOD chung
Do đó: ΔOKD đồng dạng với ΔODF
=>\(\widehat{OKD}=\widehat{ODF}\)
=>\(\widehat{ODF}=90^0\)
=>FD là tiếp tuyến của (O)

a: Xét (O) có
AB,AC là các tiếp tuyến
nên AB=AC
mà OB=OC
nên OA là trung trực của BC
Xét tứ giác OBAC có
góc OBA+góc OCA=180 độ
nên OBAC là tứ giác nội tiếp
b: Xét ΔAEC và ΔACD có
gó ACE=góc ADC
góc EAC chung
Do đo: ΔAEC đồng dạng với ΔACD
=>AE/AC=AC/AD
=>AC^2=AE*AD

a: Xét (O) có
AB,AC là các tiếp tuyến
nên AB=AC
mà OB=OC
nên OA là trung trực của BC
Xét tứ giác OBAC có
góc OBA+góc OCA=180 độ
nên OBAC là tứ giác nội tiếp
b: Xét ΔAEC và ΔACD có
gó ACE=góc ADC
góc EAC chung
Do đo: ΔAEC đồng dạng với ΔACD
=>AE/AC=AC/AD
=>AC^2=AE*AD

a
Theo giả thiết có:
`AB=AC`
`OB=OC`
=> AO là đường trung trực của đoạn BC
=> AO⊥BC
b
Ta có:
`OB=OC=R`
Gọi điểm giao nhau của BC và OA là H có:
`HB=HC`
Từ trên suy ra: HO là đường trung bình của ΔCDB
=> HO//BD
=> OA//BD (H nằm trên đoạn OA)
c
AB là tiếp tuyến đường tròn.
=> OB⊥AB
Lại có: BH⊥OA (cmt)
Áp dụng hệ thức lượng vào tam giác OAB vuông tại B, đường cao BH có:
\(\dfrac{1}{BH^2}=\dfrac{1}{AB^2}+\dfrac{1}{OB^2}\\ \Leftrightarrow\dfrac{1}{BH^2}=\dfrac{1}{8^2}+\dfrac{1}{6^2}\\ \Rightarrow BH=\sqrt{1:\left(\dfrac{1}{8^2}+\dfrac{1}{6^2}\right)}=\dfrac{24}{5}=4,8\left(cm\right)\)
\(BC=2BH\left(BH=HC\right)\\ \Rightarrow BC=2.4,8=9,6\left(cm\right)\)


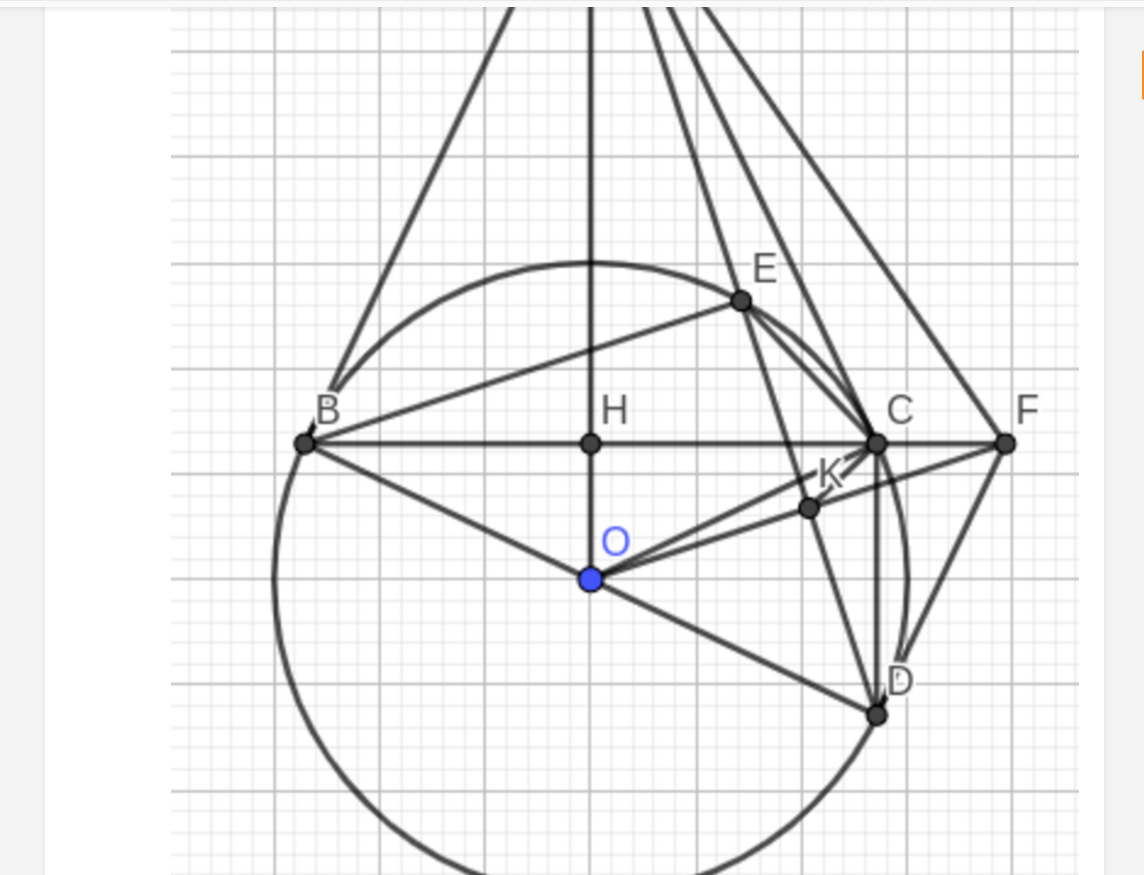
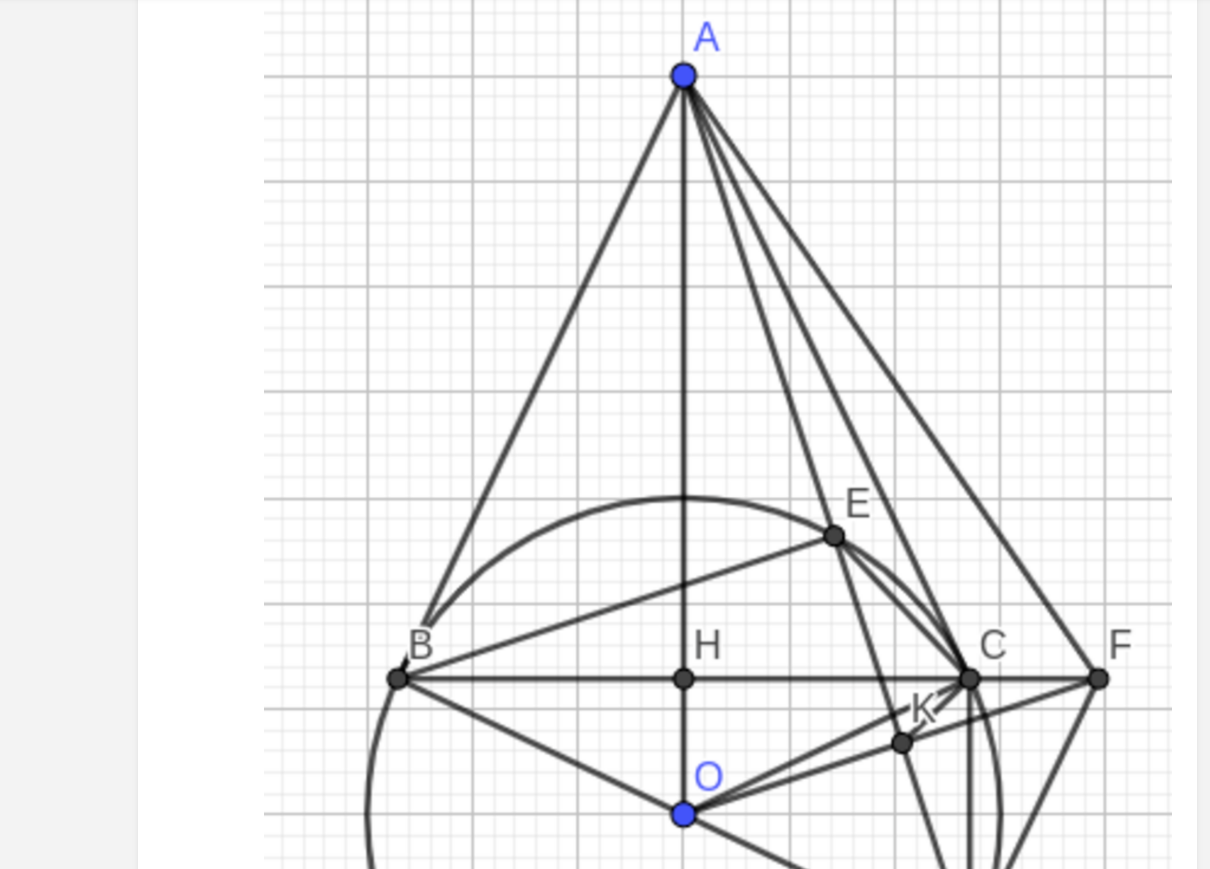
a: Xét (O) có
AB là tiếp tuyến
AC là tiếp tuyến
Do đó: AB=AC
hay A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
nên O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA⊥BC