Cho \(\widehat{xOy}\) = 60o . Trên các tia Ox,Oy lần lượt lấy các điểm A,B (A,B khác O ) . Trên đoạn thẳng AB lấy điểm C sao cho \(\widehat{AOC}\) = 30o
a) Tính số đo \(\widehat{BOC}\)
b) Từ O vẽ tia Oz sao cho \(\widehat{COz}\) = 90o . Tính số đo \(\widehat{AOz}\)
( cố gắng giúp mk câu b)

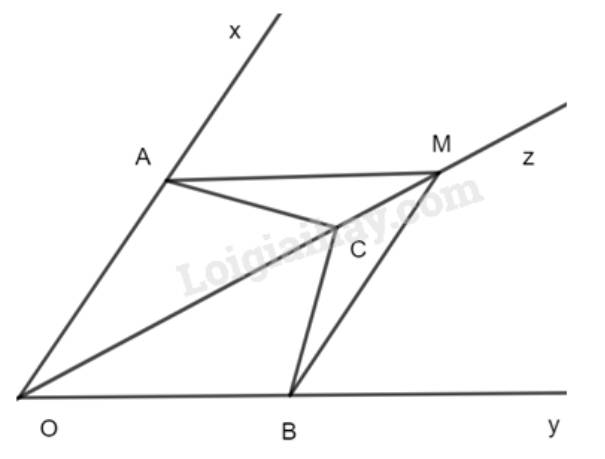
a) Vì điểm C nằm giữa hai điểm A và B nên tia OC nằm giữa hai tia OA và OB
\(\Leftrightarrow\widehat{AOC}+\widehat{BOC}=\widehat{AOB}\)
\(\Leftrightarrow\widehat{BOC}+30^0=60^0\)
hay \(\widehat{BOC}=30^0\)
Vậy: \(\widehat{BOC}=30^0\)
bạn giúp mk câu b nữa đc không ?