=> [x^2013+y^2013]^2 = 4.x^2012.y^2012

[x^2013+y^2013]^2 \(\ge\)4.x^2013.y^2013= >4.x^2012.y^2012\(\ge\)4.x^2013.y^2013 => 1 \(\ge\) xy => 1-xy \(\ge\) 0

Dấu bằng xảy ra khi x=y= 1

Vậy min 1-xy = 0 khi x=y=1

- Với \(xy=0\Rightarrow P=1\)

- Với \(xy\ne0\):

Bình phương giả thiết:

\(4x^{2012}y^{2012}=\left(x^{2013}+y^{2013}\right)^2\ge4x^{2013}y^{2013}\)

\(\Rightarrow4x^{2012}y^{2012}\left(1-xy\right)\ge0\)

\(\Rightarrow1-xy\ge0\)

\(\Rightarrow P_{min}=0\) khi \(x=y=1\)

Dễ này á anh ;;-;;

Ta có: \(A=2013-xy\Leftrightarrow y=\frac{2013-A}{x}\)

Đặt \(2013-A=B\)thì ta có \(y=\frac{B}{x}\)(1)

Theo đề bài có

\(5x^2+\frac{y^2}{4}+\frac{1}{4x^2}=\frac{5}{2}\)

\(\Leftrightarrow5x^2+\frac{B^2}{4x^2}+\frac{1}{4x^2}=\frac{5}{2}\)

\(\Leftrightarrow20x^4-10x^2+B^2+1=0\)

Để PT có nghiệm (theo biến x²) thì \(\Delta\ge0\)

\(\Leftrightarrow5^2-20\left(B^2+1\right)\ge0\)

\(\Leftrightarrow B^2\le0,25\Leftrightarrow-0,5\le B\le0,5\)

\(\Leftrightarrow-0,5\le2013-A\le0,5\)

\(\Leftrightarrow2012,5\le A\le2013,5\)

Đạt GTLN khi \(\left(x,y\right)=\left(\frac{1}{2},-1;-\frac{1}{2},1\right)\)

Đạt GTNN khi \(\left(x;y\right)=\left(\frac{1}{2},1;-\frac{1}{2},-1\right)\)

\(B=\frac{x^3}{y+1}+\frac{y^3}{1+x}=\frac{\left(x^4+y^4\right)+\left(x^3+y^3\right)}{xy+x+y+1}\)

\(=\frac{\left(x^4+y^4\right)+\left(x+y\right)\left(x^2+y^2-xy\right)}{x+y+2}=\frac{\left(x^4+y^4\right)+\left(x+y\right)\left(x^2+y^2-1\right)}{x+y+2}\)

Áp dụng BĐT cô si với các số dương x² ; y² ; x⁴ ; y⁴ ta được :

\(B\ge\frac{2x^2y^2+\left(x+y\right)\left(2xy-1\right)}{x+y+2}=\frac{2+\left(x+y\right)}{x+y+2}=1\)

Dấu ''='' xảy ra khi \(\Leftrightarrow x=y=1\)

Áp dụng BĐT Cô-si:

X⁴+1\(\ge\) 2X²   Dấu = xảy ra <=> X=1

Y⁴ + 1\(\ge\)  2Y²  Dấu = xảy ra <=> Y=1

=> P\(\ge\)  2X² . 2Y²+2013

        \(\ge\)   4X²Y² +2013 

Vì 4X²Y²\(\ge\)    0

=> P    \(\ge\)    2013

Vậy Min P= 2013 tại X=Y=1

Chọn đáp án C

Phương pháp

Biến đổi giả thiết để tìm mối liên hệ của x theo y. Thay vào biểu thức P rồi sử dụng phương pháp hàm số để tìm giá trị nhỏ nhất của P.

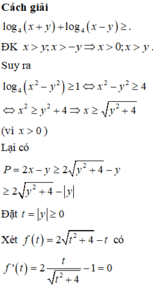
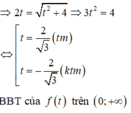
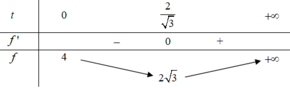
\(y\ge\dfrac{8-x}{x+1}\Rightarrow P\ge4x+\dfrac{8-x}{x+1}+3=\dfrac{4x^2+6x+11}{x+1}=\dfrac{4x^2-4x+1+10\left(x+1\right)}{x+1}=\dfrac{\left(2x-1\right)^2}{x+1}+10\ge10\)

\(P_{min}=10\) khi \(\left(x;y\right)=\left(\dfrac{1}{2};5\right)\)

\(P=\dfrac{x^2+y^2+6}{x+y}=\dfrac{x^2+y^2+2xy+4}{x+y}=\dfrac{\left(x+y\right)^2+4}{x+y}=x+y+\dfrac{4}{x+y}\)

\(P\ge2\sqrt{\left(x+y\right).\dfrac{4}{x+y}}=4\)

\(P_{min}=4\) khi \(x=y=1\)