Khoảng cách giữa người nói và bức tường để nghe rõ được tiếng vang:

Để có được tiếng vang thì thời gian nghe được âm phản xạ cách âm trực tiếp là \(\frac{1}{15}\)giây.

Vậy khoảng cách ngắn nhất ( S_min ) từ người nói đến bức tường để nghe được tiếng vang bằng quãng đường âm truyền. Do đó:

S_min= \(\frac{s}{2}\)= \(\frac{v.t}{2}\)=\(\frac{340.\frac{1}{15}}{2}\)=11,39 (m)

Kết luận: Có tiếng vang khi ta nghe thấy âm phản xạ cách âm phát ra 1 khoảng thời gian ít nhất là \(\frac{1}{15}\) giây.

^^ngo ngoc ly

1/ 5 hay 1/15 z bnngo ngoc ly

Để nghe được tiếng vang thì thời gian nghe được âm phản xạ cách âm trực tiếp ít nhất là  giây.

Quãng đường truyền đi và về trong \(\dfrac{1}{15}\) giây là : 

Do quãng đường âm truyền từ người đến tường bị phản xạ trên tường và truyền về đến tai người dài gấp đôi khoảng cách từ người đến tường nên khoảng cách ngắn nhất từ người đến tường là : 

a, Trong cả 2 phòng đều có âm phản xạ .

b, Để nghe được tiếng vang thì thời gian âm truyền từ chỗ người nói đến bức tường là:

\(t=\frac{1}{15}:2=\frac{1}{30}\)(s)

Khoảng cách ngắn nhất từ chỗ người nói đến bức tường là:

\(S=v.t=340.\frac{1}{30}\approx11,3\)(m) Vậy Khoảng cách ngắn nhất từ chỗ người nói đến bức tường là 11,3(m)

Mk vẫn chưa hiểu lắm! Có thể giảng lại giúp mk nhóe!!??

a) Trong cả hai phòng đều có âm phản xạ. Khi em nói trong phòng nhỏ, mặc dù vẫn có âm phản xạ từ tường phòng đến tai nhưng em không nghe được tiếng vang vì âm phản xạ từ tường phòng và âm nói ra đến tai em gần như cùng một lúc hoặc khoảng chênh lệch thời gian giữa âm phản xạ và âm trực tiếp nhỏ hơn 1/15 giây.

b) Vì âm phát ra từ nguồn âm đi quảng đường S (bằng khoảng cách từ người đến tường) đến tường, rồi sau đó bị tường phản xạ và truyền âm phản xạ về tai người, âm phản xạ đi thêm quảng đường S về tai người. Như vậy âm đã đi một đường S1 = 2S rồi mới về tai người.

Để tạo tiếng vang thì âm dội lại phải đến tai phải chậm hơn âm truyền trực tiếp đến tai một khoảng thời gian ít nhất là 1/15 giây.

Quãng đường truyền đi và truyền về trong 1/15 giây là:

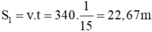
Vì S1 = 2S nên khoảng cách ngắn nhất giữa người nói và bức tường để nghe rõ được tiếng vang là:

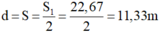
Kết luận: Có tiếng vang khi ta nghe thấy âm phản xạ cách với âm phát ra một khoảng ít nhất là 1/15s.

Vận tốc truyền âm \(v=340\)m/s

Để nghe đc tiếng vang sau ít nhất \(\dfrac{1}{15}s\) thì lại truyền âm ngược lại.Quãng đường truyền âm là:

\(2S=340\cdot\dfrac{1}{15}=\dfrac{68}{3}\)\(\Rightarrow S=\dfrac{34}{3}m\)

\(s=\dfrac{v.t}{2}=\dfrac{340.\dfrac{1}{15}}{2}=11,3333\left(m\right)\)

Khoảng cách giữa người nói và bức tường để nghe rõ được tiếng vang:

Để có được tiếng vang thì thời gian nghe được âm phản xa cách âm trực tiếp là giây.

Vậy khoảng cách ngắn nhất (S_min) từ người nói đến bức tường để nghe được tiếng vang bằng quãng đường âm truyền. Do đó:

S_min = = 11,39m)

Kết luân: Có tiếng vang khi ta nghe thấy âm phản xạ cách âm phát ra một khoảng thời gian ít nhất là giây.

Khoảng cách ngắn nhất từ người nói đến bức tường là:

340:2=170m

Vậy khoảng cách ngắn nhất từ người nói đến bức tường để nghe được tiếng vang là 170m

b, Khoảng cách ít nhất để nghe được tiếng vang :

\(s=\dfrac{vt}{2}=\dfrac{340\cdot\dfrac{1}{15}}{2}=11,3\left(3\right)\left(m\right)\)

Để nghe được tiếng vang thì thời gian truyền phải \(\ge\dfrac{1}{15}s\)

Khoảng cách ngắn nhất:

\(v=\dfrac{2s}{t}\rightarrow2s=v.t\rightarrow s=\dfrac{v.t}{2}=\dfrac{340.\dfrac{1}{15}}{2}=\dfrac{34}{3}\approx11,33\left(m\right)\)