Tất cả các giá trị x thỏa mãn (x + 3). x = 0 là:
x = 3
x = 0
x ∈ {0; -3}
x ∈ {0; 3}
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TN
3 tháng 11 2016
Câu 1:(3x+2)(4x-5)=0
\(\Leftrightarrow\orbr{\begin{cases}3x+2=0\\4x-5=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=-\frac{2}{3}\\x=\frac{5}{4}\end{cases}}\)
Câu 2:
x3+5x2+3x-9=0
<=>x3+6x2+9x-x2-6x-9=0
<=>x(x2+6x+9)-(x2+6x+9)=0
<=>(x-1)(x2+6x+9)=0
<=>(x-1)(x+3)2=0
\(\Leftrightarrow\orbr{\begin{cases}x-1=0\\\left(x+3\right)^2=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=1\\x=-3\end{cases}}\)
TN
3 tháng 11 2016
Câu 2: bổ sung thêm phần cuối
Tổng các giá trị x thỏa mãn là (-3)+1=-2
CM
6 tháng 10 2017
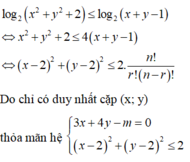
nên đường thẳng 3x + 4y - m = 0 là tiếp tuyến của đường tròn (x – 2)2 + (y – 2)2 = 2.
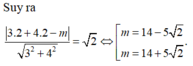
Chọn C.
LS
1
16 tháng 12 2016
\(x^3+5x^2+3x-9=0\)
\(=>x^3-x^2+6x^2-6x+9x-9=0\)
\(=>x^2\left(x-1\right)+6x\left(x-1\right)+9\left(x-1\right)=0\)
\(=>\left(x-1\right)\left(x^2+6x+9\right)=0\)
\(=>\left(x-1\right)\left(x+3\right)^2=0\)
\(=>\orbr{\begin{cases}x-1=0\\x+3=0\end{cases}}\)
\(=>\orbr{\begin{cases}x=1\\x=-3\end{cases}}\)
VT
1
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 4 2023
\(x\left(3x-2\right)-3x^2=\dfrac{3}{4}\)
\(\Leftrightarrow3x^2-2x-3x^2=\dfrac{3}{4}\)
\(\Leftrightarrow-2x=\dfrac{3}{4}\)
\(\Leftrightarrow x=\dfrac{3}{4}:\left(-2\right)\)
\(\Leftrightarrow x=-\dfrac{3}{8}\)
Chọn C