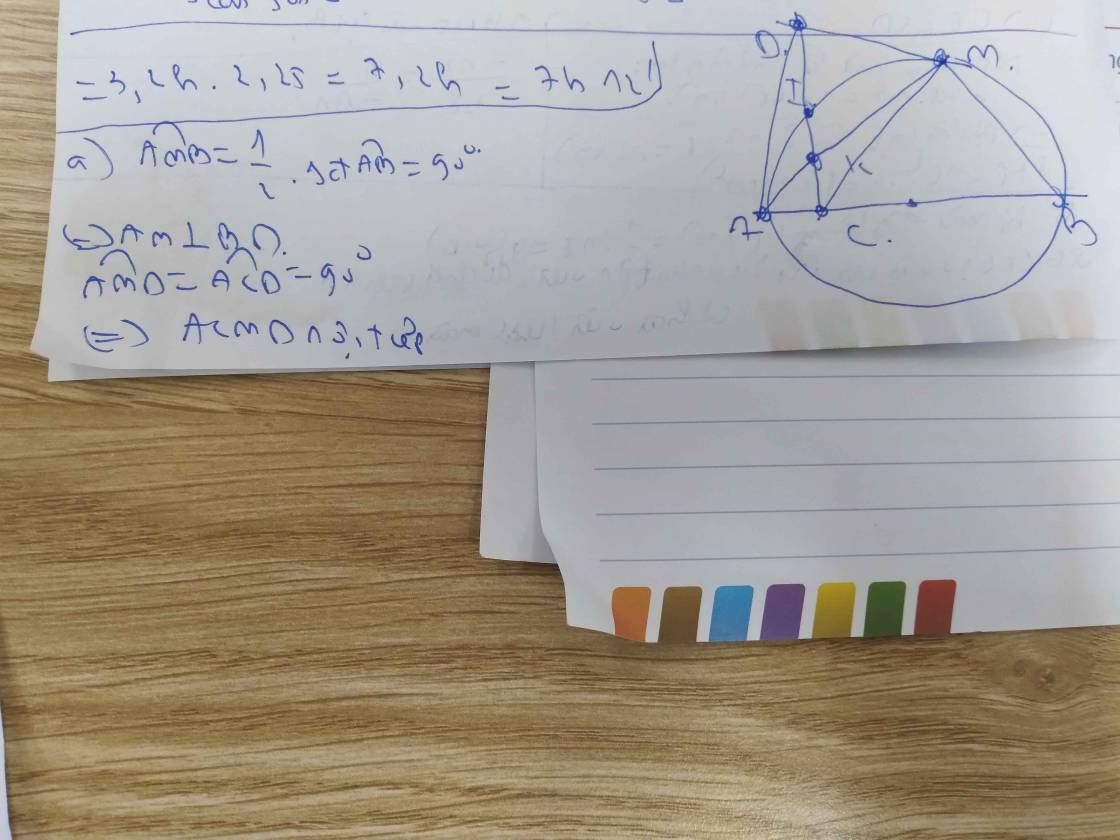
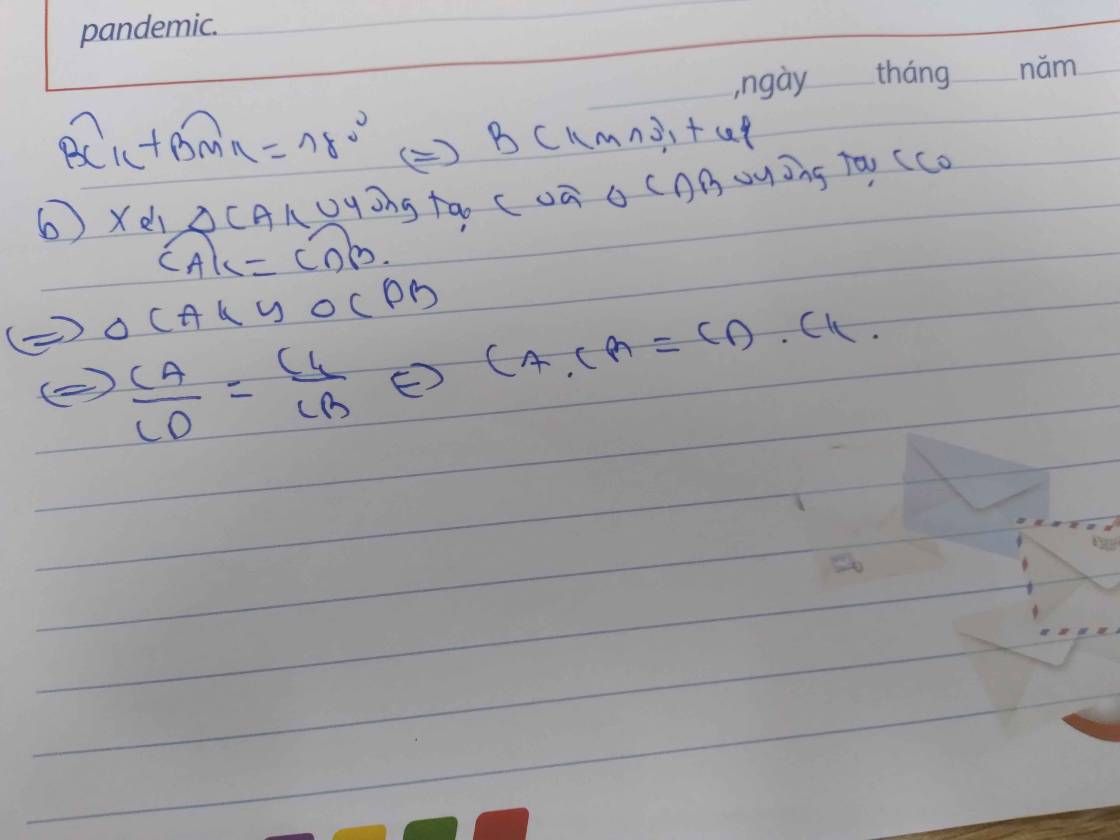Giải hộ mình bài này nhé. Mình cần RẤT GẤP!!!!!!! : Cho nửa đường tròn tâm O đường kính AB. C là một điểm nằm giữa O và A. Đường thẳng vuông góc với AB tại C cắt nửa đường tròn trên tại I. K là một điểm bất kì nằm trên đoạn thẳng CI (K khác C và I), tia AK cắt nửa đường tròn (O) tại M, tia BM cắt CI tại D. Chứng minh: a) Tứ giác ACMD, BCKM nội tiếp đường tròn. b) CK.CD=CA.CB c) Gọi giao điểm của AD và nửa đường tròn (O) là N. Chứng minh B,K,N thẳng hàng. d) Tâm đường tròn ngoại tiếp tam giác AKD nằm trên một đường thẳng cố định khi K di động trên đoạn thẳng CI.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1:
góc AMB=1/2*sđ cung AB=90 độ
=>AM vuông góc BD
góc ACD=góc AMD=90 độ
=>ACMD nội tiếp
góc KCB+góc KMB=180 độ
=>BMKC nội tiếp
2: Xét ΔCAK vuông tại C và ΔCDB vuông tại C có
góc CAK=góc CDB
=>ΔCAK đồng dạng với ΔCDB
=>CA/CD=CK/CB
=>CA*CB=CD*CK

Vi NN nằm trên (O)(O) nên ˆNAB=90∘NAB^=90∘(1) ⇒NB⊥DA⇒NB⊥DA. Mà DC⊥AB,AM⊥DBDC⊥AB,AM⊥DB ⇒K⇒K Là trực tâm tam giác DABDAB suy ra BK⊥ADBK⊥AD (2). Từ (1) và (2) suy ra B,N,KB,N,K thẳng hàng

a) Xét (O) có
ΔAMB nội tiếp đường tròn(A,M,B\(\in\)(O))
AB là đường kính(gt)
Do đó: ΔMAB vuông tại M(Định lí)
\(\Leftrightarrow AM\perp MB\) tại M
\(\Leftrightarrow AM\perp BD\) tại M
\(\Leftrightarrow\widehat{AMD}=90^0\)
Xét tứ giác ADMC có
\(\widehat{AMD}=\widehat{ACD}\left(=90^0\right)\)
\(\widehat{AMD}\) và \(\widehat{ACD}\) là hai góc cùng nhìn cạnh AD
Do đó: ADMC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)