cho a3+b3+c3=3abc. Tính Q=\(\dfrac{a^2}{a^2-b^2-c^2}+\dfrac{b^2}{b^2-c^2-a^2}+\dfrac{c^2}{c^2-a^2-b^2}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1.
Theo nguyên lý Dirichlet, trong 3 số a;b;c luôn có 2 số cùng phía so với \(\dfrac{2}{3}\), không mất tính tổng quát, giả sử đó là b và c
\(\Rightarrow\left(b-\dfrac{2}{3}\right)\left(c-\dfrac{2}{3}\right)\ge0\)
Mặt khác \(0\le a\le1\Rightarrow1-a\ge0\)
\(\Rightarrow\left(b-\dfrac{2}{3}\right)\left(c-\dfrac{2}{3}\right)\left(1-a\right)\ge0\)
\(\Leftrightarrow-abc\ge\dfrac{4a}{9}+\dfrac{2b}{3}+\dfrac{2c}{3}-\dfrac{2ab}{3}-\dfrac{2ac}{3}-bc-\dfrac{4}{9}\)
\(\Leftrightarrow-abc\ge-\dfrac{2a}{9}+\dfrac{2}{3}\left(a+b+c\right)-\dfrac{2ab}{3}-\dfrac{2ac}{3}-bc-\dfrac{4}{9}=-\dfrac{2a}{9}-\dfrac{2ab}{3}-\dfrac{2ac}{3}-bc+\dfrac{8}{9}\)
\(\Leftrightarrow-2abc\ge-\dfrac{4a}{9}-\dfrac{4ab}{3}-\dfrac{4ac}{3}-2bc+\dfrac{16}{9}\)
\(\Leftrightarrow ab+bc+ca-2abc\ge-\dfrac{4a}{9}-\dfrac{ab}{3}-\dfrac{ac}{3}-bc+\dfrac{16}{9}\)
\(\Leftrightarrow ab+bc+ca-2abc\ge-\dfrac{4a}{9}-\dfrac{a}{3}\left(b+c\right)-bc+\dfrac{16}{9}\ge-\dfrac{4a}{9}-\dfrac{a}{3}\left(2-a\right)-\dfrac{\left(b+c\right)^2}{4}+\dfrac{16}{9}\)
\(\Rightarrow ab+bc+ca-2abc\ge-\dfrac{4a}{9}+\dfrac{a^2}{3}-\dfrac{2a}{3}-\dfrac{\left(2-a\right)^2}{4}+\dfrac{16}{9}\)
\(\Rightarrow ab+bc+ca-2abc\ge\dfrac{a^2}{12}-\dfrac{a}{9}+\dfrac{7}{9}=\dfrac{1}{12}\left(a-\dfrac{2}{3}\right)^2+\dfrac{20}{27}\ge\dfrac{20}{27}\)
\(\Rightarrow ab+bc+ca\ge2abc+\dfrac{20}{27}\)
Dấu "=" xảy ra khi \(a=b=c=\dfrac{2}{3}\)

Bài 1:
$a^3+b^3+c^3=3abc$
$\Leftrightarrow (a+b)^3-3ab(a+b)+c^3-3abc=0$
$\Leftrightarrow [(a+b)^3+c^3]-[3ab(a+b)+3abc]=0$
$\Leftrightarrow (a+b+c)[(a+b)^2-c(a+b)+c^2]-3ab(a+b+c)=0$
$\Leftrightarrow (a+b+c)[(a+b)^2-c(a+b)+c^2-3ab]=0$
$\Leftrightarrow (a+b+c)(a^2+b^2+c^2-ab-bc-ac)=0$
$\Rightarrow a+b+c=0$ hoặc $a^2+b^2+c^2-ab-bc-ac=0$
Xét TH $a^2+b^2+c^2-ab-bc-ac=0$
$\Leftrightarrow 2(a^2+b^2+c^2)-2(ab+bc+ac)=0$
$\Leftrightarrow (a-b)^2+(b-c)^2+(c-a)^2=0$
$\Rightarrow a-b=b-c=c-a=0$
$\Leftrightarrow a=b=c$
Vậy $a^3+b^3+c^3=3abc$ khi $a+b+c=0$ hoặc $a=b=c$
Áp dụng vào bài:
Nếu $a+b+c=0$
$A=\frac{-c}{c}+\frac{-b}{b}+\frac{-a}{a}=-1+(-1)+(-1)=-3$
Nếu $a=b=c$
$P=\frac{a+a}{a}+\frac{b+b}{b}+\frac{c+c}{c}=2+2+2=6$

T a c ó : a 3 - b 3 + c 3 + 3 a b c = ( a 3 + c 3 + 3 a 2 c + 3 a c 2 ) - 3 a 2 c - 3 a c 2 + 3 a b c - b 3 = ( a + c ) 3 - b 3 - 3 a c ( a + c - b ) = ( a + c - b ) [ ( a + c ) 2 + b ( a + c ) + b 2 ] - 3 a c ( a + c - b ) = ( a + c - b ) ( a 2 + b 2 + c 2 + a b + b c - a c ) ( a + b ) 2 + ( b + c ) 2 + ( c - a ) 2 = ( a 2 + 2 a b + b 2 ) + ( b 2 + 2 b c + c 2 ) + ( c 2 - 2 a c + a 2 ) = 2 a 2 + 2 b 2 + 2 c 2 + 2 a b + 2 b c - 2 a c = 2 ( a 2 + b 2 + c 2 + a b + b c - a c )
= > C = (a + c − b)(a 2 + b 2 + c 2 + ab + bc − ac) 2(a 2 + b 2 + c 2 + ab + bc − ac) = a + c − b 2
Mà a + c - b = 10 nên C = a + c − b 2 = 10 2 = 5
Đáp án D

Do \(a^3+b^3+c^3=3abc\)
\(\Rightarrow a^3+b^3+c^3-3abc=0\)
\(\Rightarrow\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ac\right)=0\)
Mà \(a+b+c\ne0\)
\(\Rightarrow a^2+b^2+c^2-ab-bc-ac=0\)
\(\Rightarrow a^2+b^2+c^2=ab+bc+ac\)
Khi đó:
\(\left(a+b+c\right)^2=a^2+b^2+c^2+2\left(ab+bc+ac\right)\)\(=\left(a^2+b^2+c^2\right)+2\left(a^2+b^2+c^2\right)=3\left(a^2+b^2+c^2\right)\)
Vậy: \(N=\frac{a^2+b^2+c^2}{\left(a+b+c\right)^2}=\frac{a^2+b^2+c^2}{3\left(a^2+b^2+c^2\right)}=\frac{1}{3}\)


Có:
\(a^3+b^3+c^3=3abc\\\Leftrightarrow a^3+b^3+c^3-3abc=0\\\Leftrightarrow (a+b)^3+c^3-3ab(a+b)-3abc=0\\\Leftrightarrow (a+b+c)^3-3(a+b)c(a+b+c)-3ab(a+b+c)=0\\\Leftrightarrow (a+b+c)[(a+b+c)^2-3(a+b)c-3ab]=0\\\Leftrightarrow (a+b+c)(a^2+b^2+c^2+2ab+2bc+2ac-3ac-3bc-3ab)=0\\\Leftrightarrow (a+b+c)(a^2+b^2+c^2-ab-bc-ac)=0\\\Leftrightarrow a^2+b^2+c^2-ab-bc-ac=0(vì.a+b+c\ne0)\\\Leftrightarrow 2a^2+2b^2+2c^2-2ab-2bc-2ac=0\\\Leftrightarrow (a^2-2ab+b^2)+(b^2-2bc+c^2)+(a^2-2ac+c^2)=0\\\Leftrightarrow (a-b)^2+(b-c)^2+(a-c)^2=0\)
Ta thấy: \(\left\{{}\begin{matrix}\left(a-b\right)^2\ge0\forall a,b\\\left(b-c\right)^2\ge0\forall b,c\\\left(a-c\right)^2\ge0\forall a,c\end{matrix}\right.\)
\(\Rightarrow\left(a-b\right)^2+\left(b-c\right)^2+\left(a-c\right)^2\ge0\forall a,b,c\)
Mà: \(\left(a-b\right)^2+\left(b-c\right)^2+\left(a-c\right)^2=0\)
nên: \(\left\{{}\begin{matrix}a-b=0\\b-c=0\\a-c=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=b\\b=c\\a=c\end{matrix}\right.\Leftrightarrow a=b=c\)
Thay \(a=b=c\) vào \(A\), ta được:
\(A=\dfrac{\left(2016+\dfrac{a}{a}\right)+\left(2016+\dfrac{b}{b}\right)+\left(2016+\dfrac{c}{c}\right)}{2017^3}\left(a,b,c\ne0\right)\)
\(=\dfrac{2016+1+2016+1+2016+1}{2017^3}\)
\(=\dfrac{2016\cdot3+1\cdot3}{2017^3}\)
\(=\dfrac{3\cdot\left(2016+1\right)}{2017^3}\)
\(=\dfrac{3}{2017^2}\)
Vậy: ...
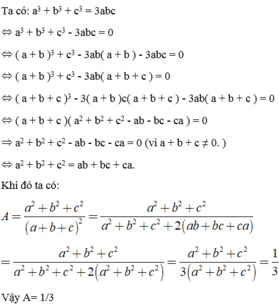
Ta có: \(a^3+b^3+c^3=3abc\)
\(\Leftrightarrow a^3+b^3+c^3-3abc=0\)
\(\Leftrightarrow\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc=0\)
\(\Leftrightarrow\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2\right)-3ab\left(a+b+c\right)=0\)
\(\Leftrightarrow\left(a+b+c\right)\left(a^2+b^2+c^2-ab-ac-bc\right)=0\)
\(\Leftrightarrow\left(a+b+c\right)\left(2a^2+2b^2+2c^2-2ab-2ac-2bc\right)=0\)
\(\Leftrightarrow\left(a+b+c\right)\left[\left(a-b\right)^2+\left(b-c\right)^2+\left(a-c\right)^2\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a+b+c=0\\\left(a-b\right)^2+\left(b-c\right)^2+\left(a-c\right)^2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a+b+c=0\\a=b=c\end{matrix}\right.\)
Trường hợp 1: a+b+c=0
\(\Leftrightarrow\left\{{}\begin{matrix}a=-\left(b+c\right)\\b=-\left(a+c\right)\\c=-\left(a+b\right)\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a^2=b^2+2bc+c^2\\b^2=a^2+2ac+c^2\\c^2=a^2+2ab+b^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a^2-b^2-c^2=2bc\\b^2-a^2-c^2=2ac\\c^2-a^2-b^2=2ab\end{matrix}\right.\)
\(\Leftrightarrow Q=\dfrac{a^2}{2bc}+\dfrac{b^2}{2ac}+\dfrac{c^2}{2ab}=\dfrac{a^3+b^3+c^3}{2abc}=\dfrac{3abc}{2abc}=\dfrac{3}{2}\)
Trường hợp 2: a=b=c
\(\Leftrightarrow Q=\dfrac{a^2}{a^2-a^2-a^2}+\dfrac{b^2}{b^2-b^2-b^2}+\dfrac{c^2}{c^2-c^2-c^2}\)
\(\Leftrightarrow Q=\dfrac{a^2}{-2a^2}+\dfrac{b^2}{-2b^2}+\dfrac{c^2}{-2c^2}=\dfrac{-1}{2}+\dfrac{-1}{2}+\dfrac{-1}{2}=\dfrac{-3}{2}\)