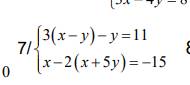\(A=\dfrac{1}{4}\left(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{n^2}\right)\)

=>\(A< \dfrac{1}{4}\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{n-1}-\dfrac{1}{n}\right)\)

=>A<1/4*1=1/4

3. Tóm tắt:

\(m_1=1,5kg\)

\(t_1=100^oC\)

\(m_2=200g=0,2kg\)

\(m_3=2,5kg\)

\(t_2=20^oC\)

\(c_1=380J/kg.K\)

\(c_2=880J/kg.K\)

\(c_3=4200J/kg.K\)

===========

a) \(t=?^oC\)

b) \(t'=70^oC\)

\(Q'=?J\)

Giải:

a) Nhiệt độ cuối cùng của nước:

\(Q_1=Q_2+Q_3\)

\(\Leftrightarrow m_1.c_1.\left(t_1-t\right)=\left(t-t_2\right)\left(m_2.c_2+m_3.c_3\right)\)

\(\Leftrightarrow1,5.380.\left(100-t\right)=\left(t-20\right)\left(0,2.880+2,5.4200\right)\)

\(\Leftrightarrow57000-570t=10676t-213520\)

\(\Leftrightarrow57000+213520=10676t+570t\)

\(\Leftrightarrow270520=11246t\)

\(\Leftrightarrow t=\dfrac{270520}{11246}=24,05^oC\)

b) Nhiệt lượng cần cung cấp để đun nóng nước:

\(Q'=\left(m_1.c_1+m_2.c_2+m_3.c_3\right).\left(t'-t\right)\)

\(\Leftrightarrow Q'=\left(1,5.880+0,2.880+2,5.4200\right)\left(70-24,05\right)\)

\(\Leftrightarrow Q'=11246.45,95\)

\(\Leftrightarrow Q'=516753,7J\)

1. Tóm tắt:

\(m=300kg\)

\(\Rightarrow P=10m=3000N\)

\(h=1,5m\)

\(s=6m\)

\(F=1250N\)

==========

a) \(A_i=?J\)

b) \(A_{tp}=?J\)

c) \(H=?\%\)

\(F_{ms}=?N\)

Giải:

a) Công có ích thực hiện được:

\(A_i=P.h=3000.1,5=4500J\)

b) Công toàn phần thực hiện được:

\(A_{tp}=F.s=1250.6=7500J\)

c) Hiệu suất mặt phẳng nghiêng:

\(H=\dfrac{A_i}{A_{tp}}.100\%=\dfrac{4500}{7500}.100\%=60\%\)

Công của lực ma sát:

\(A_{ms}=A_{tp}-A_i=7500-4500=3000J\)

Độ lớn của lực ma sát:

\(A_{ms}=F_{ms}.s\Rightarrow F_{ms}=\dfrac{A_{ms}}{s}=\dfrac{3000}{6}=500N\)

thi ko giúp 

B

điểm trung bình là

8 nha bạn

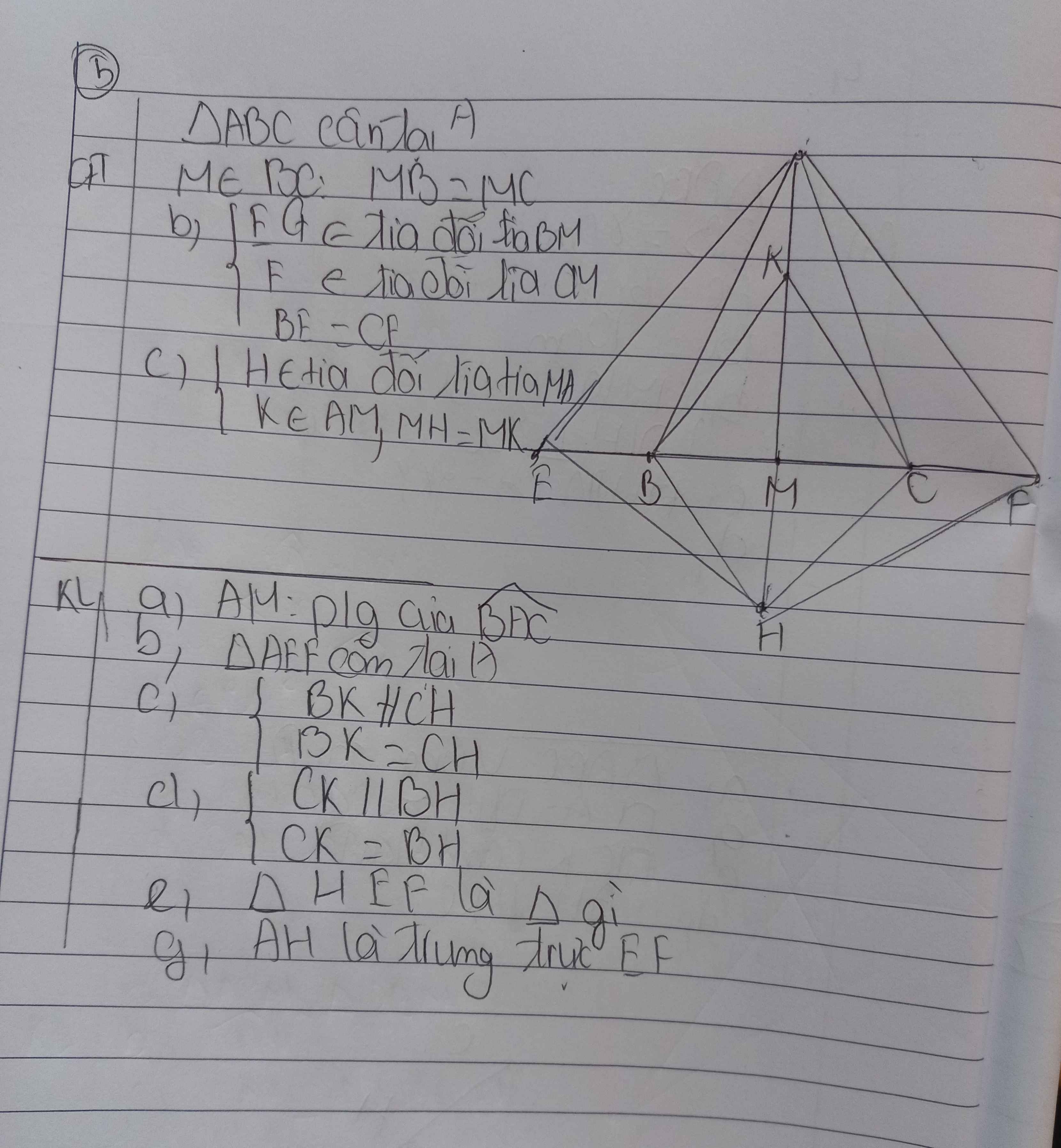
a: Ta có: ΔABC cân tại A

mà AM là đường trung tuyến

nên AM là đường phân giác

b: Xét ΔABE và ΔACF có 

AB=AC

\(\widehat{ABE}=\widehat{ACF}\)

BE=CF

Do đó: ΔABE=ΔACF

c: Xét tứ giác BKCH có 

M là trung điểm của BC

M là trung điểm của HK

Do đó: BKCH là hình bình hành

Suy ra: BK//CH; BK=CH

d: Ta có: BKCH là hình bình hành

nên CK//BH; CK=BH

sửa lại nhé

\(\left\{{}\begin{matrix}3\left(x-y\right)-y=11\\x-2\left(x+5y\right)=-15\end{matrix}\right.\)

\(< =>\left\{{}\begin{matrix}3x-3y-y=11\\x-2x-10y=-15\end{matrix}\right.\)

\(< =>\left\{{}\begin{matrix}3x-4y=11\\-x-10y=-15\end{matrix}\right.\)

\(< =>\left\{{}\begin{matrix}x=5\\y=1\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}3x-3y-y=11\\x-2x-10y=-15\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}3x-4y=11\\-x-10y=-15\left(1\right)\end{matrix}\right.\)

Nhân \(-3\) vào \(\left(1\right)\)

\(\left\{{}\begin{matrix}3x-4y=11\left(2\right)\\3x+30y=45\left(3\right)\end{matrix}\right.\)

Lấy \(\left(2\right)-\left(3\right)\) :

\(\Leftrightarrow3x-3x-4y-30y=11-45\)

\(\Leftrightarrow-34y=-34\)

\(\Leftrightarrow x=1\)

Lấy \(x=1\) thay vào \(\left(2\right)\) : \(3.1-4y=11\Leftrightarrow y=2\)

Vậy hệ pt có nghiệm duy nhất \(\left(x;y\right)=\left(1;2\right)\)