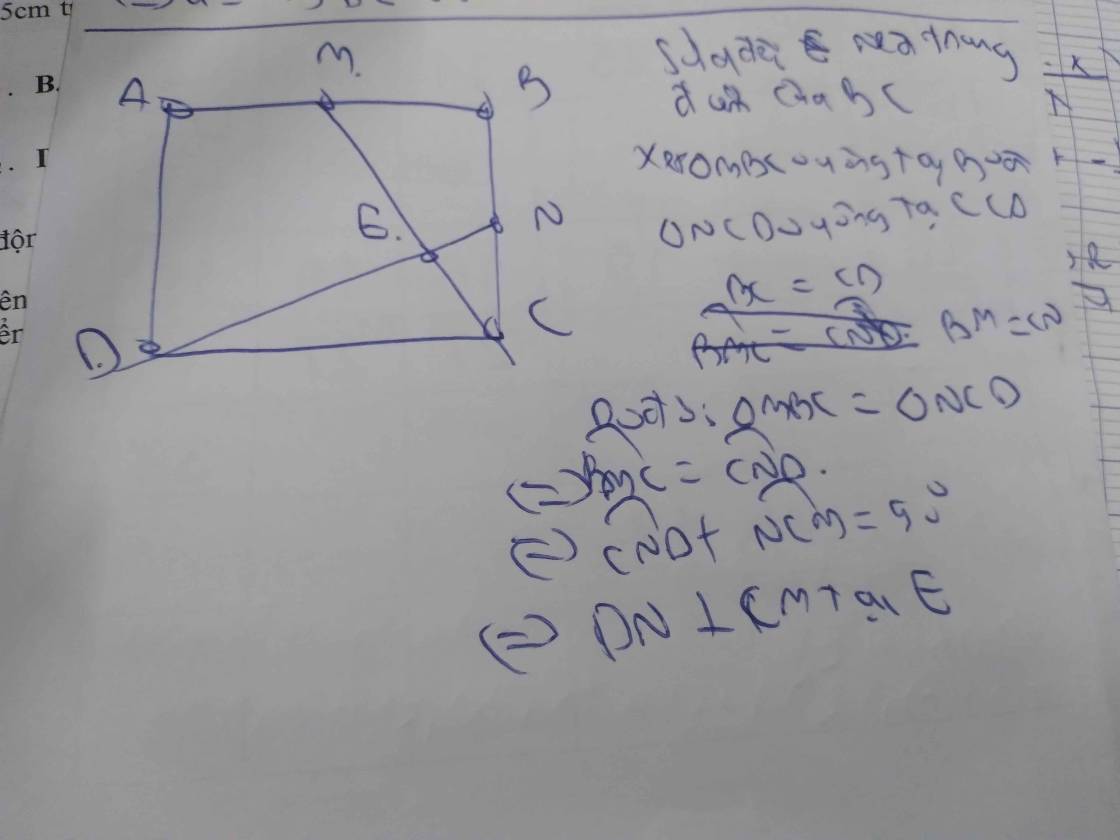
Bài 5: Cho hình vuông ABCD. Gọi M, N lần lượt là trung điểm của AD và DC a) Chứng minh AN vuông góc với BM. b) Gọi E là trung điểm DN; J là giao điểm của AN và BE. Chứng minh MJ vuông góc với BE
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a/ Ta có
AB=BC và MA=MB; NB=NC => MB=NC
Xét hai tg vuông BMC và tg vuông CNC có
MB=NC (cmt)
BC=CD (cạnh hình vuông)
=> tg BMC= tg CND => ^BMC=^CND (1)
Trong tg vuông BMC có ^BCM+^BMC=90 (2)
Từ (1) và (2) => ^BCM+^CND=90 => ^CHN=90 => MC vuông góc DN
b/
Ta có AB=CD (cạnh hình vuông) và MA=MB; KC=KD => MA=KC
Mà MA//KC
=> AMCK là hình bình hành => AK//MC (3)
Xét tg CDH có ID=IH và KD=KC (đề bài) => IK là đường trung bình => IK//MC (4)
Từ (3) và (4) => AK trùng với IK => A; I; K thẳng hàng
c/
Xét tg ADH có
AI//MC mà MC vuông góc với DN => AI vuông góc với DN => AI là đường cso của tg ADH (5)
Ta có ID=IH (đề bài) => AI là trung tuyến của tg ADH (6)
Từ (5) và (6) => tg ADH cân tại A (tam giác có đường cao đồng thời là đường trung tuyến ... là tam giác cân)

Đề sai rồi bạn. E là giao của CM và DN thì E trùng với C rồi bạn
Cho hình vuông ABCD. Gọi M , N lần lượt là trung điểm của AB và BC ĐÂY Ạ

a: Xét tứ giác ANMD có
AN//MD
AN=MD
AN=AD
=>ANMD là hình thoi
Xét tứ giác BCMN co
BN//CM
BN=CM
BN=BC
=>BCMN là hình thoi
b: Xét ΔNCD có
NM là trung tuyến
NM=CD/2
=>ΔNCD vuông tại N
c: Xét ΔAHD vuông tại H và ΔCND vuông tại N có
góc ADH=góc CDN
=>ΔAHD đồng dạng với ΔCND