Gọi các số đó là  

+ Do x chia hết cho 4 nên 2 chữ số tận cùng của x phải chia hết cho 4

+ Các bộ 2 chữ số ( được tạo ra từ các số đã cho) và chia hết cho 4 là {20, 40, 12, 52, 72, 24}.

+ Với  = 20 ta có 4 cách chọn a; 3 cách chọn b nên có 4.3 = 20 số thỏa mãn trường hợp này

Tương tự khi cd = 40; có 20 số.

+ Với  = 12; ta có 3 cách chọn a và 3 cách chọn b nên có 3.3 = 9 số thỏa mãn .

Tương tự khi = 52; 72; 24 mỗi trường hợp có 9 số.

Vậy có 20 + 20 + 9 + 9 + 9 + 9 = 76 số

  Chọn B.

Đáp án B

Số cần lập có dạng  a b c d ¯

trong đó  a ;   b ;   c ;   d ∈ 0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6

trong đó  d = 0 ; 5

TH1: d = 0  khi đó a,b,c có A 6 3  cách chọn và sắp xếp.

TH2: d = 0 khi đó a,b,c có 5.5.4 ( a # 0 )  cách chọn và sắp xếp

Theo quy tắc cộng có

A 6 3 + 5 . 5 . 4 = 220  số thỏa mãn yêu cầu bài toán

Đáp án B.

Số cần lập có dạng a b c d ¯  trong đó a ; b ; c ; d ∈ 0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; trong đó d = {0;5}.

TH1: d = 0 khi đó a,b,c có A 6 3  cách chọn và sắp xếp.

TH2: d = 5 khi đó a,b,c có 5.5.4 a ≠ 0  cách chọn và sắp xếp.

Theo quy tắc cộng có A 6 3 + 5 . 5 . 4 = 220  số thỏa mãn yêu cầu bài toán.

Ta có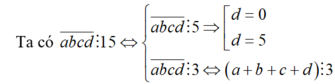  

• TH1.  

Mỗi bộ sau đều lập được 6 số: (1;2;3),(1;2;6),(1;3;5),(1;5;6),(2;3;7),(2;6;7),(3;5;7),(5;6;7)

• TH2.  

Mỗi bộ sau đều lập được 4 số: (0;1;3);(0;1;6);(0;6;7).

Mỗi bộ sau đều lập được 6 số: (1;2;7);(1;3;6); (3;6;7)

Tóm lại có tất cả 6.8+4.4+6.3=82 số thỏa mãn.

Chọn B.

Chọn A

A

2:

\(\overline{abcd}\)

d có 1 cách chọn 

a có 3 cách chọn

b có 2 cách chọn

c có 1 cách chọn

=>Có 3*2*1*1=6 cách

1: \(\overline{abc}\)

a có 3 cách

b có 3 cách

c có 2 cách

=>Có 3*3*2=18 cách

Chữ số cuối cùng bằng 0, các khả năng với 2 chữ số là

(1;2); (1;8); (4;5); (1;5); (2;4); (4;8).

Chữ số cuối cùng bằng 5, các khả năng xảy ra với 2 chữ số là

(1;0);(4;0);(1;3); (2;8);(3;4).

Hoán vị các bộ 2 chữ số không tồn tại số 0, như vậy có 6.2 + 2 + 3.2 = 20 số.

Chọn B.

Chữ số cuối cùng bằng 0, các khả năng với 2 chữ số hàng trăm và hàng chục là (1;2); (1;8); (4;5); (1;5); (2;4); (4;8).

Chữ số cuối cùng bằng 5, các khả năng xảy ra với 2 chữ số hàng trăm và hàng chục là (1;0);(4;0);(1;3);(2;8);(3;4).

Hoán vị các bộ 2 chữ số không tồn tại số 0, như vậy có 6.2+2+3.2=20  số.

 Chọn B.

Chữ số cuối cùng bằng 0; các cặp số có thể xảy ra là (1;2),(1;5),(1;8),(2;4),(4;5),(4;8).  (0;1),(0;4),(1; 3),(2;5),(3;8)

Trường hợp này có 2!.6=12 số.

Chữ số cuối bằng 2 ta có các bộ (1;0),(4;0),(1; 3),(3;4),(5;8), hoán vị được  

2!.3+2=8 số.

Chữ số cuối bằng 4 ta có các bộ (2;0),(2; 3),(3;5),(3;8), hoán vị được 2!.3+1=7 số.

Chữ số cuối bằng 8 ta có các bộ (0;1),(0;4),(1; 3),(2;5),(3;4) hoán vị được 2!.3+2=8 số.

Kết hợp lại ta có 12+8+7+8= 35 số.

Chọn C