Giúp mình câu này với ạ,xin cảm ơn nhièu
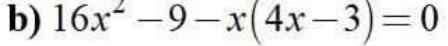
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(=\dfrac{5(x+4)}{(x+4)(x-4)}+\dfrac{4(x-4)}{(x+4)(x-4)}-\dfrac{2x-24}{(x+4)(x-4)} \\=\dfrac{7x+28}{(x+4)(x-4)} \\=\dfrac{7(x+4)}{(x+4)(x-4)} \\=\dfrac{7}{x-4}\)
b: \(=\dfrac{5x+20+4x-16-2x+24}{\left(x-4\right)\left(x+4\right)}=\dfrac{7x+28}{\left(x-4\right)\left(x+4\right)}=\dfrac{7}{x-4}\)


Hàm bậc 2 có \(\left\{{}\begin{matrix}a=1>0\\-\dfrac{b}{2a}=6-m\end{matrix}\right.\) nên nghịch biến trên khoảng \(\left(-\infty;6-m\right)\)
Hàm nghịch biến trên khoảng đã cho khi:
\(6-m\ge2\Rightarrow m\le4\)
\(\Rightarrow\) Có 4 giá trị nguyên dương của m


1: Xét tứ giác BHCK có
CH//BK
BH//CK
Do đó: BHCK là hình bình hành
Suy ra: Hai đường chéo BC và HK cắt nhau tại trung điểm của mỗi đường
mà M là trung điểm của BC
nên M là trung điểm của HK
2: Gọi giao điểm của IH và BC là O
Suy ra: IH\(\perp\)BC tại O và O là trung điểm của IH
Xét ΔHIK có
O là trung điểm của HI
M là trung điểm của HK
Do đó: OM là đường trung bình của ΔHIK
Suy ra: OM//IK
hay BC//IK
mà BC\(\perp\)IH
nên IH\(\perp\)IK
Xét ΔHOC vuông tại O và ΔIOC vuông tại O có
OC chung
HO=IO
Do đó: ΔHOC=ΔIOC
Suy ra: CH=CI
mà CH=BK
nên CI=BK
Xét tứ giác BCKI có IK//BC
nên BCKI là hình thang
mà CI=BK
nên BCKI là hình thang cân


a: \(=\dfrac{x+2}{x+2}=1\)
b: \(=\dfrac{2x+6}{x+3}=2\)

9b:
Kẻ OK vuông góc SA tại K
BD vuông góc AC
BD vuông góc SO
=>BD vuông góc (SAC)
=->BD vuông góc SA
mà OK vuông góc SA
nên SA vuông góc (BKD)
=>SA vuông góc BK; SA vuông góc KD
=>((SAB); (SAD))=(BK;KD)
ΔSAC vuông cân tại O nên OK=1/2SA=a/căn 3
ΔBKD cso KO=BO=OD=a/căn 3=1/2*BD
=>ΔBKD vuông tại K
=>góc BKD=90 độ
=>(SAB) vuông góc (SAD)

1)\(6x-x^2=x\left(6-x\right)\)
2)\(5x^2z-15xyz+30xz^2=5x\left(xz-3y+6z\right)\)
3)\(x^3-6x^2+9x=x\left(x^2-6x+9\right)=x\left(x-3\right)^2\)
\(\Leftrightarrow\left(4x-3\right)\left(4x+3-x\right)=0\)
=>(4x-3)(3x+3)=0
=>x=3/4 hoặc x=-1