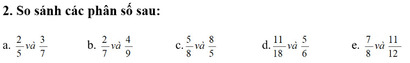a,bc.3=m2,bn

\(\frac{m2,bn}{3}=a,bc\) 

m khong chia duoc cho 3=> m2 chia 3 =a

m khac 2 khac 0=> m=1=> a=4

b chia cho 3 =b => b=9 hoac 0

n chia cho 3=c vay n=3, 9 hoac 6   voi n=3=> c=1 (loai vi co m=1);

 n=6 => c=2 (loai)

vay n=9=> c=3  

KL

a=4; b=0; c=3; m=1; n=9

thu lai

4,03x3=12,09

lik e mình 3 cái nha mình giải

aaaaa96 chia hết cho 3 và 8

aaaaa96 chia hết cho 3 vì 96 chia hết cho 3 => a x 5 chia hết cho 3 => a = 3;6;9

aaaaa96 chia hết cho 8 suy ra a96 chia hết cho 8

Nếu a = 3 => 396 : 8 không chia hết cho 8 (loại)

Nếu a = 6 => 696 : 8 chia hết cho 8

Nếu a = 9 => 996 : 8 không chia hết cho 8

Vậy a = 6

\(B=x^2-x\)

\(B=x^2-2\cdot x\cdot\frac{1}{2}+\left(\frac{1}{2}\right)^2-\left(\frac{1}{2}\right)^2\)

\(B=\left(x-\frac{1}{2}\right)^2-\frac{1}{4}\)

mà \(\left(x-\frac{1}{2}\right)^2\ge0\forall x\)

\(\Rightarrow B\ge\frac{1}{4}\forall x\)

Dấu "=" xảy ra \(\Leftrightarrow x-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{2}\)

Vậy Bmin = 1/4 <=> x = 1/2

P.s : đây là tìm B min

Còn cách nữa tìm Bmax :v

Vì \(x^2\ge0\forall x\)

\(\Rightarrow B\le x\forall x\)

Dấu "=" xảy ra \(\Leftrightarrow x^2=0\Leftrightarrow x=0\)

Vậy Bmax = 0 <=> x = 0

xác xuất để tổng tổng chẵn là 33,33%

So chan

Muốn tick vô đây trl nha!

\(\dfrac{2}{5}< \dfrac{3}{7}\)

\(\dfrac{2}{7}< \dfrac{4}{9}\)

\(\dfrac{5}{8}< \dfrac{8}{5}\)

\(\dfrac{11}{18}< \dfrac{5}{6}\)

\(\dfrac{7}{8}< \dfrac{11}{12}\)

#)Giải : 

Đặt \(\frac{a}{b}=\frac{c}{d}=k\Rightarrow\hept{\begin{cases}a=bk\\c=dk\end{cases}}\left(#\right)\)

Thay vào VP, ta được :

\(\frac{ab}{cd}=\frac{bk.b}{dk.d}=\frac{b^2k}{d^2k}=\frac{b^2}{d^2}\left(1\right)\)

Lại có : 

\(\frac{a^2+b^2}{c^2+d^2}\Rightarrow\frac{a^2}{c^2}=\frac{b^2}{d^2}\Rightarrow a^2d^2=b^2c^2\Rightarrow\frac{a^2}{b^2}=\frac{c^2}{d^2}=\left(\frac{a}{b}\right)^2=\left(\frac{c}{d}\right)^2=\left(\frac{a+b}{c+d}\right)^2\)

Tiếp tục thay (#) vào, ta được :

\(\left(\frac{bk+b}{dk+d}\right)^2=\left(\frac{b^2\left(k+1\right)}{d^2\left(k+1\right)}\right)^2=\frac{b^2}{d^2}\left(2\right)\)

Từ (1) và (2) \(\Rightarrow\frac{a^2+b^2}{c^2+d^2}=\frac{b^2}{d^2}=\frac{ab}{cd}\Rightarrow\frac{a^2+b^2}{c^2+d^2}=\frac{ab}{cd}\left(đpcm\right)\)

Có \(\frac{a}{b}=\frac{c}{d}\Rightarrow\frac{a^2}{b^2}=\frac{c^2}{d^2}\Rightarrow\frac{a^2}{c^2}=\frac{b^2}{d^2}\)\(=\frac{a^2+b^2}{c^2+d^2}\)\(\left(1\right)\)

Có \(\frac{a}{b}=\frac{c}{d}\Rightarrow\frac{a}{c}=\frac{b}{d}\Rightarrow\frac{a}{c}.\frac{a}{c}=\frac{b}{d}.\frac{a}{c}\)\(\Rightarrow\frac{a^2}{c^2}=\frac{ab}{cd}\)\(\left(2\right)\)

Từ \(\left(1\right)\)và\(\left(2\right)\)\(\RightarrowĐPCM\)