tinh gia tri bieu thuc biet 12x^2+20x+1. biet 3x^2+5x-2=0. mn lam jup nhe
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: \(\Delta'=32>0\)
\(\Rightarrow\) Phương trình có 2 nghiệm phân biệt
Theo Vi-ét, ta có: \(\left\{{}\begin{matrix}x_1+x_2=12\\x_1x_2=4\end{matrix}\right.\)
Mặt khác: \(T=\dfrac{x_1^2+x^2_2}{\sqrt{x_1}+\sqrt{x_2}}\)
\(\Rightarrow T^2=\dfrac{x_1^4+x^4_2+2x_1^2x_2^2}{x_1+x_2+2\sqrt{x_1x_2}}=\dfrac{\left(x_1^2+x_1^2\right)^2}{x_1+x_2+2\sqrt{x_1x_2}}\) \(=\dfrac{\left[\left(x_1+x_2\right)^2-2x_1x_2\right]^2}{x_1+x_2+2\sqrt{x_1x_2}}=\dfrac{\left(12^2-2\cdot4\right)^2}{12+2\sqrt{4}}=1156\)
Mà ta thấy \(T>0\) \(\Rightarrow T=\sqrt{1156}=34\)

b, Ta co: \(x^3+xy^2-x^2y-y^3+3\)
\(=\left(x^3-y^3\right)+\left(xy^2-x^2y\right)+3\)
\(=\left(x-y\right)^3+3xy\left(x-y\right)-xy\left(x-y\right)+3\)
= 3 ( vì x-y = 0)


x^2=a;y^2=b( Đk:a,b không âm)
Từ giả thiết suy ra a+b=2
=>3x^4+5x^2y^2+2y^4+2y^2
=3a^2+5ab+2b^2+2b
=(3a^2+3ab)+(2ab+2b^2)+2b
=3a(a+b)+2b(a+b)+2b
=(a+b)(3a+2b)+2b
=2(3a+2b)+2b
=2(2a+2b)+2a+2b
=4.2+2.2=12


x^2=a;y^2=b(Đk:a,b không âm)
Từ giả thiết suy ra a+b=2
=>3x^4+5x^2y^2+2y^4+2y^2
=3a^2+5ab+2b^2+2b
=(3a^2+3ab)+(2ab+2b^2)+2b
=3a(a+b)+2b(a+b)+2b
=(a+b)(3a+2b)+2b
=2(3a+2b)+2b
=2(2a+2b)+2a+2b
=4.2+2*\.2=12
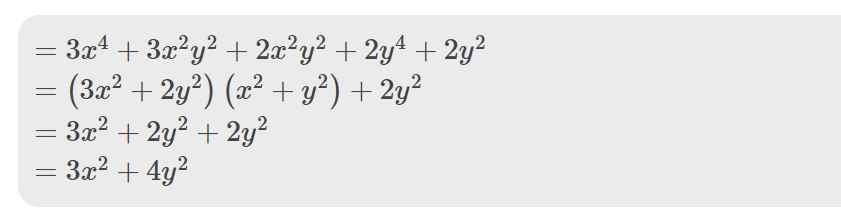
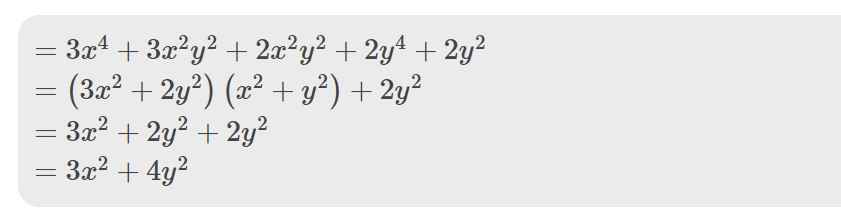
Ta có \(3x^2+5x-2=0\Rightarrow12x^2+20x-8=0\)
\(\Rightarrow12x^2+20x=8\)
thay vào biểu thức đầu tiên ta được
\(12x^2+20x+1=8+1=9\)