Một khẩu súng bắn với vận tốc 12m/giây.Hỏi phải mất bao nhiêu phút để viên đạn của khẩu súng đó găm vào một mảnh bia cách đó 720m?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


- Mổi khẩu súng bắn hết 100 viên đạn có số thời gian là:
0.5 * 100 = 50 (giây).
- 10 khẩu súng bắn hết thì có số thời gian là:
50 * 10 = 500 (giây) = 8 phút 20 giây
Đáp số: 8 phút 20 giây.

Theo định luật bảo toàn động lượng ta có:
m . v → + M . V → = 0 → ⇒ V → = − m M v → ⇒ V = − m M = − 3 m / s
Vậy súng giật lùi với vận tốc 3m/s ngược chiều với hướng viên đạn.
Chọn đáp án D

Theo định luật bảo toàn động lượng ta có:
m . v → + M . V → = 0 → ⇒ V → = − m M v →
Vậy súng giật lùi với vận tốc 3m/s ngược chiều với hướng viên đạn.

Khoảng cách từ người bắn đến tấm bia :
\(s=\dfrac{v.t}{2}=\dfrac{340.3}{2}=\dfrac{1020}{2}=510\left(m\right)\)

a) Gọi vận tốc trước và sau của khẩu súng lần lượt là v1 và v’1
Vận tốc của viên đạn trước và sau lần lượt là v2 và v’2
Khối lượng của khẩu súng M = 4 kg; khối lượng của viên đạn là m = 6 g = 0,006 kg
Ban đầu viên đạn và khẩu súng đứng yên nên v1 = v2 = 0.
Sau khi viên đạn được bắn thì v’2 = 320 m/s
Chọn chiều dương là chiều chuyển động của viên đạn
Áp dụng định luật bảo toàn động lượng ta có:
\(\begin{array}{l}\sum {\overrightarrow {{p_{tr}}} = \sum {\overrightarrow {{p_s}} } } \Leftrightarrow M.\overrightarrow {{v_1}} + m.\overrightarrow {{v_2}} = M.\overrightarrow {v_1'} + m.\overrightarrow {v_2'} \\ \Leftrightarrow M.\overrightarrow {v_1'} + m.\overrightarrow {v_2'} = \overrightarrow 0 \end{array}\)
Chiếu lên chiều dương ta có:
\(\begin{array}{l} - M.v_1' + m.v_2' = 0 \Leftrightarrow v_1' = \frac{m}{M}.v_2'\\ \Rightarrow v_1' = \frac{{0,006}}{4}.320 = 0,48(m/s)\end{array}\)
Vậy tốc độ giật lùi của súng là 0,48 m/s.
b) Tốc độ giật lùi của người và súng như nhau, coi người và súng là một hệ
Gọi vận tốc trước và sau của hệ người và khẩu súng lần lượt là v1 và v’1
Vận tốc của viên đạn trước và sau lần lượt là v2 và v’2
Khối lượng của người và khẩu súng là M = 4 + 75 = 79 kg; khối lượng của viên đạn là m = 6 g = 0,006 kg
Ban đầu viên đạn, người và khẩu súng đứng yên nên v1 = v2 = 0.
Sau khi viên đạn được bắn thì v’2 = 320 m/s
Chọn chiều dương là chiều chuyển động của viên đạn
Áp dụng định luật bảo toàn động lượng ta có:
\(\begin{array}{l}\sum {\overrightarrow {{p_{tr}}} = \sum {\overrightarrow {{p_s}} } } \\ \Leftrightarrow M.\overrightarrow {{v_1}} + m.\overrightarrow {{v_2}} = M.\overrightarrow {v_1'} + m.\overrightarrow {v_2'} \\ \Leftrightarrow M.\overrightarrow {v_1'} + m.\overrightarrow {v_2'} = \overrightarrow 0 \end{array}\)
Chiếu lên chiều dương ta có:
\(\begin{array}{l} - M.v_1' + m.v_2' = 0 \Leftrightarrow v_1' = \frac{m}{M}.v_2'\\ \Rightarrow v_1' = \frac{{0,006}}{{79}}.320 = 0,024(m/s)\end{array}\)
Vậy tốc độ giật lùi của người là 0,024 m/s.

Đề cho sai khối lượng đạn rồi phải không? =))
Bảo toàn động lượng theo phương ngang:
\(m_s\overrightarrow{v_s}+m_đ\overrightarrow{v_đ}=0\)
\(\Rightarrow\overrightarrow{v_s}=\dfrac{-m_đ\overrightarrow{v_đ}}{m_s}\Rightarrow v_s=\dfrac{-m_đv_đ}{m_s}=-1200\left(m/s\right)\)
súng giật ghê phết :)) dự đoán đạn chỉ nặng tầm 10g thôi :D
thay lại: \(v_s=\dfrac{-m_đ.v_đ}{m_s}=-1,2\left(m/s\right)\)
Vậy độ lớn vận tốc súng là -1,2 m/s ngược với chiều chuyển động của viên đạn
à độ lớn thì bỏ dấu -1,2 thành 1,2 cho mình nhé :D độ lớn không âm sorry bạn


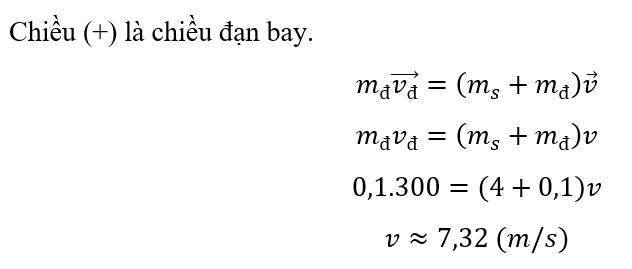
Để viên đạn của khẩu súng đó găm vào một mảnh bia cách đó 720m cần:
720 : 12 = 60 ( giây ) = 1 ( phút )
Đ/s: ...
Thời gian để viên đạn đó găm vào mảnh bia là:
720:12=60(giây)
Đổi:60 giây=1 phút
Đáp số:1 phút
ai k mình mình k lại