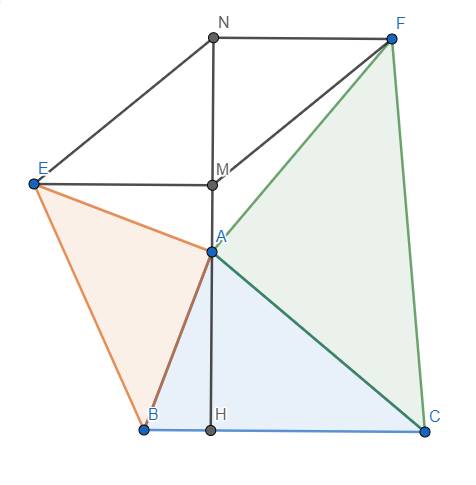
Cho tam giac ABCcos ba góc nhọn, đường cao AH. Vẽ về phía ngoài tam giac ABC các tam giác ABE và ACF vuông cân tại A. Từ E và F kẻ đường vuông góc EK và FN với đường thẳng HA
a, chứng minh rằng EK=FN.
b, gọi I là giao điểm của EF với đường thẳng HA. Tìm đièu kiện cua tam giac ABC để EF=2AI