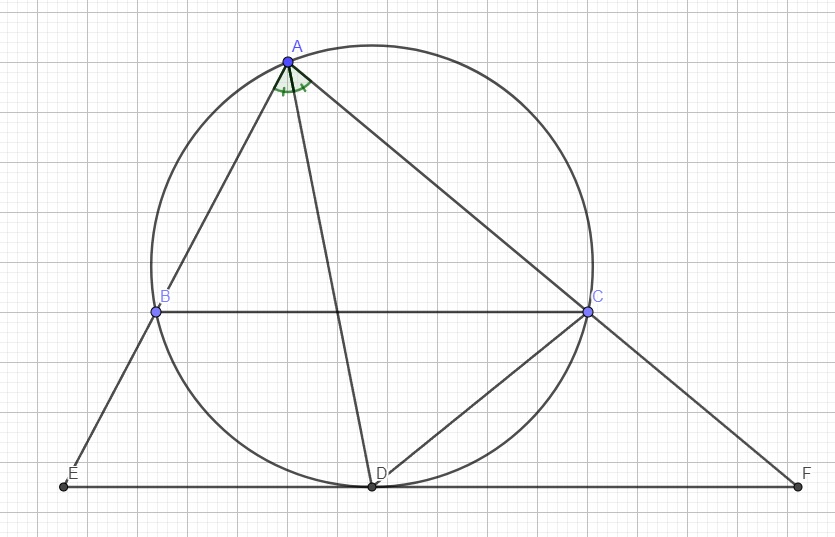
cho tam giác ABC nội tiếp đường tròn (O,R). Phân giác góc BAC cắt BC tại D và cắt đường tròn (O) tại E.Vẽ đường tròn đường kính AE. Đường thẳng qua D vuông góc với AE cắt đường kinhs AE tại F. chứng minh tam giác EFC cân
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
GN
27 tháng 5 2018
B1, a, Xét tứ giác AEHF có: góc AFH = 90o ( góc nội tiếp chắn nửa đường tròn)
góc AEH = 90o (góc nội tiếp chắn nửa đường tròn )
Góc CAB = 90o ( tam giác ABC vuông tại A)
=> tứ giác AEHF là hcn(đpcm)
b, do AEHF là hcn => cũng là tứ giác nội tiếp => góc AEF = góc AHF ( hia góc nội tiếp cùng chắn cung AF)
mà góc AHF = góc ACB ( cùng phụ với góc FHC)
=> góc AEF = góc ACB => theo góc ngoài tứ giác thì tứ giác BEFC là tứ giác nội tiếp (đpcm)
c,gọi M là giao điểm của AI và EF
ta có:góc AEF = góc ACB (c.m.t) (1)
do tam giác ABC vuông tại A và có I là trung điểm của cạng huyền CB => CBI=IB=IA
hay tam giác IAB cân tại I => góc MAE = góc ABC (2)
mà góc ACB + góc ABC + góc BAC = 180o (tổng 3 góc trong một tam giác)
=> ACB + góc ABC = 90o (3)
từ (1) (2) và (3) => góc AEF + góc MAE = 90o
=> góc AME = 90o (theo tổng 3 góc trong một tam giác)
hay AI uông góc với EF (đpcm)
CM
10 tháng 8 2017
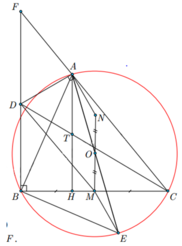
b) CD đi qua trung điểm của đường cao AH của D ABC
· Gọi F là giao của BD và CA.
Ta có BD.BE= BA.BM (cmt)
= > B D B A = B M B E = > Δ B D M ~ Δ B A E ( c − g − c ) = > B M D = B E A
Mà BCF=BEA(cùng chắn AB)
=>BMD=BCF=>MD//CF=>D là trung điểm BF
· Gọi T là giao điểm của CD và AH .
DBCD có TH //BD = > T H B D = C T C D (HQ định lí Te-let) (3)
DFCD có TA //FD = > T A F D = C T C D (HQ định lí Te-let) (4)
Mà BD= FD (D là trung điểm BF ) (5)
· Từ (3), (4) và (5) suy ra TA =TH ÞT là trung điểm AH .
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 1
Ta có: \(\widehat{CDF}=\widehat{CAD}\) (cùng chắn AD)
\(\widehat{CAD}=\widehat{BAD}\) (AD là phân giác)
\(\widehat{BAD}=\widehat{BCD}\) (cùng chắn BD)
\(\Rightarrow\widehat{CDF}=\widehat{BCD}\)
\(\Rightarrow BC||EF\) (hai góc so le trong bằng nhau)
\(\Rightarrow\dfrac{AB}{AE}=\dfrac{AC}{AF}\Rightarrow AB.AF=AC.AE\)
Cũng từ BC song song EF \(\Rightarrow\widehat{ACB}=\widehat{AFD}\) (đồng vị)
Mà \(\widehat{ACB}=\widehat{ADB}\) (cùng chắn AB)
\(\Rightarrow\widehat{AFD}=\widehat{ADB}\)
Xét 2 tam giác AFD và ADB có:
\(\left\{{}\begin{matrix}\widehat{FAD}=\widehat{DAB}\left(\text{AD là phân giác}\right)\\\widehat{AFD}=\widehat{ADB}\left(cmt\right)\end{matrix}\right.\) \(\Rightarrow\Delta AFD\sim\Delta ADB\left(g.g\right)\)
\(\Rightarrow\dfrac{AD}{AB}=\dfrac{AF}{AD}\Rightarrow AB.AF=AD^2\)
\(\Rightarrow AB.AF=AC.AE=AD^2\)
