Cho đa thức \(A=\frac{1}{3}\)\(x^2y^3+y^6+x^5y^8\)và đơn thức \(B=2x\). Không tính chia đa thức , hay xem xét A có chia hết cho B không
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Hạng tử y 6 của đa thức A không chia hết cho đơn thức B = 2x.
Do đó, đa thức A không chia hết cho đơn thức B
Chọn đáp án A

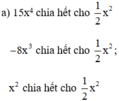
Do đó A = 15x4 - 8x3 + x2 chia hết cho 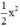 hay A chia hết cho B.
hay A chia hết cho B.
b) A = x2 - 2x + 1 = (x – 1)2
Vậy A chia hết cho x – 1 hay A chia hết cho B.

Lời giải của bạn Hà sai, lời giải của bạn Quang đúng.
Vì 5x4 chia hết cho 2x2;
–4x3 chia hết cho 2x2;
6x2y chia hết cho 2x2
Do đó A = 5x4 – 4x3 + 6x2y chia hết cho 2x2 hay A chia hết cho B.
Chú ý: Đơn thức A chia hết cho đơn thức B nếu tìm được đơn thức Q sao cho A=B.Q
Ví dụ : Cho hai đơn thức A= 2x2y3; B = 7xy
Khi đó với đơn thức 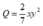 thì A=B.Q
thì A=B.Q
Do đó, đơn thức A chia hết cho đơn thức B.

Bài giải:
Ta có: A : B = (5x4 – 4x3 + 6x2y) : 2x2
= (5x2 : 2x2) + (– 4x3 : 2x2) + (6x2y : 2x2)
= x2 – 2x + 3y
Như vậy A chia hết cho B vì mọi hạng tử của A đều chia hết cho B.
Vậy: Quang trả lời đùng, Hà trả lời sai.
Ta có: A : B = (5x4 – 4x3 + 6x2y) : 2x2
= (5x2 : 2x2) + (– 4x3 : 2x2) + (6x2y : 2x2)
= 5252x2 – 2x + 3y
Như vậy A chia hết cho B vì mọi hạng tử của A đều chia hết cho B.
Vậy: Quang trả lời đùng, Hà trả lời sai.

Nhận thấy:
15xy2 chia hết cho 6y2
17xy3 chia hết cho 6y2
18y2 chia hết cho 6y2
Vậy A = 15xy2 + 17xy3 + 18y2 chia hết cho 6y2 hay A chia hết cho B.

a) A chia hết cho B vì x4, x3, x2 đều chia hết cho x2
b) A chia hết cho B, vì x2– 2x + 1 = (1 – x)2, chia hết cho 1 - x

Bài giải:
A chia hết cho B vì mỗi hạng tử của A đều chia hết cho B (mỗi hạng tử của A đều có chứa nhân tử y với số mũ lớn hơn hay bằng 2 bằng với số mũ của y trong B).
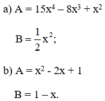
 x2
x2