Mọi người giúp e ý b, d, e với ạ e cần gấp :((
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Đặt \(a=x^2+x\)
Đa thức trở thành: \(a^2-14a+24=\left(a^2-14a+49\right)-25=\left(a-7\right)^2-25=\left(a-7-5\right)\left(a-7+5\right)=\left(a-12\right)\left(a-2\right)\)
Thay a:
\(\left(a-12\right)\left(a-2\right)=\left(x^2+x-12\right)\left(x^2+x-2\right)\)
b) Đặt \(a=x^2+x\)
Đa thức trở thành:
\(\left(x^2+x\right)^2+4x^2+4x-12=\left(x^2+x\right)^2+4\left(x^2+x\right)-12=a^2+4a-12=\left(a^2+4x+4\right)-16=\left(a+2\right)^2-16=\left(a+2-4\right)\left(a+2+4\right)=\left(a-2\right)\left(a+6\right)\)
Thay a:
\(\left(a-2\right)\left(a+6\right)=\left(x^2+x-2\right)\left(x^2+x+6\right)\)


Mình viết phần điền tiếp thui nhé, cái đề cho mk k viết
1 where they were organizing the party
2 if I knew the woman in red over there
3 Peter why he didn't turn off the light
4 she was going
5 if the nearest post office was far away
6 what we were going to do that Christmas
7 where I worked
8 how far it was from my house to my school
9 if his friend was a good person
10 how many people there were in my family
1. ...where they were organizing the party.
2. ...if I knew the woman in red over there.
3. ...Peter why he didn't turn off the light.
4. ...she was going.
5. ...if the nearest post office was far away.
6. ...what we were going to do this Christmas.
7. ...where I worked.
8. ...how far it was from my house to my school.
9. ...if his friend was a good person.
10. ...how many people there were in my family.

a: Xét tứ giác BHCK có
BK//CH
BH//CK
Do đó:BHCK là hình bình hành



\(5,\\ a,=x^4+4x^2+4-4x^2=\left(x^2+2\right)^2-4x^2=\left(x^2-2x+2\right)\left(x^2+2x+2\right)\\ b,=x^4+16x^2+64-16x^2=\left(x^2+8\right)^2-16x^2=\left(x^2-4x+8\right)\left(x^2+4x+8\right)\\ c,=x^8+x^7+x^6-x^6+x^5-x^5+x^4-x^4+x^3-x^3+x^2-x^2+x-x+1\\ =x^6\left(x^2+x+1\right)-x^4\left(x^2+x+1\right)+x^3\left(x^2+x+1\right)-x\left(x^2+x+1\right)+\left(x^2+x+1\right)\\ =\left(x^6-x^4+x^3-x+1\right)\left(x^2+x+1\right)\)
\(d,=x^8+2x^4+1-x^4=\left(x^4+1\right)^2-x^4=\left(x^4-x^2+1\right)\left(x^4+x^2+1\right)\\ =\left(x^4-x^2+1\right)\left(x^4+2x^2+1-x^2\right)\\ =\left(x^4-x^2+1\right)\left(x^2-x+1\right)\left(x^2+x+1\right)\\ e,=x^5+x^4-x^4+x^3-x^3+x^2-x^2+x+1\\ =x^3\left(x^2+x+1\right)-x^2\left(x^2+x+x\right)+\left(x^2+x+1\right)\\ =\left(x^3-x^2+1\right)\left(x^2+x+1\right)\\ f,=x^3+2x^2-x^2-2x+2x+4\\ =\left(x+2\right)\left(x^2-x+2\right)\\ g,=x^4+2x^2+1-25=\left(x^2+1\right)^2-25\\ =\left(x^2+1-5\right)\left(x^2-1-5\right)=\left(x^2-4\right)\left(x^2-6\right)=\left(x-2\right)\left(x+2\right)\left(x^2-6\right)\)
\(h,=x^3-2x^2+2x^2-4x+2x-4=\left(x-2\right)\left(x^2+2x+2\right)\\ i,=a^4-4a^2b^2+4b^4-4a^2b^2=\left(a^2-2b^2\right)^2-4a^2b^2\\ =\left(a^2-2ab-2b^2\right)\left(a^2+2ab-2b^2\right)\)

áp dụng đl ta-lét vào tam giác có:
\(\dfrac{BC}{CA}=\dfrac{DE}{EA}=\dfrac{BC}{5}=\dfrac{3}{8}=>BC=\dfrac{3}{8}.5=\dfrac{15}{8}=1,875\)
X = BC + CA = 1,875 + 5 = 6,875


 mọi người giúp e với ạ e đang cần gấp
mọi người giúp e với ạ e đang cần gấp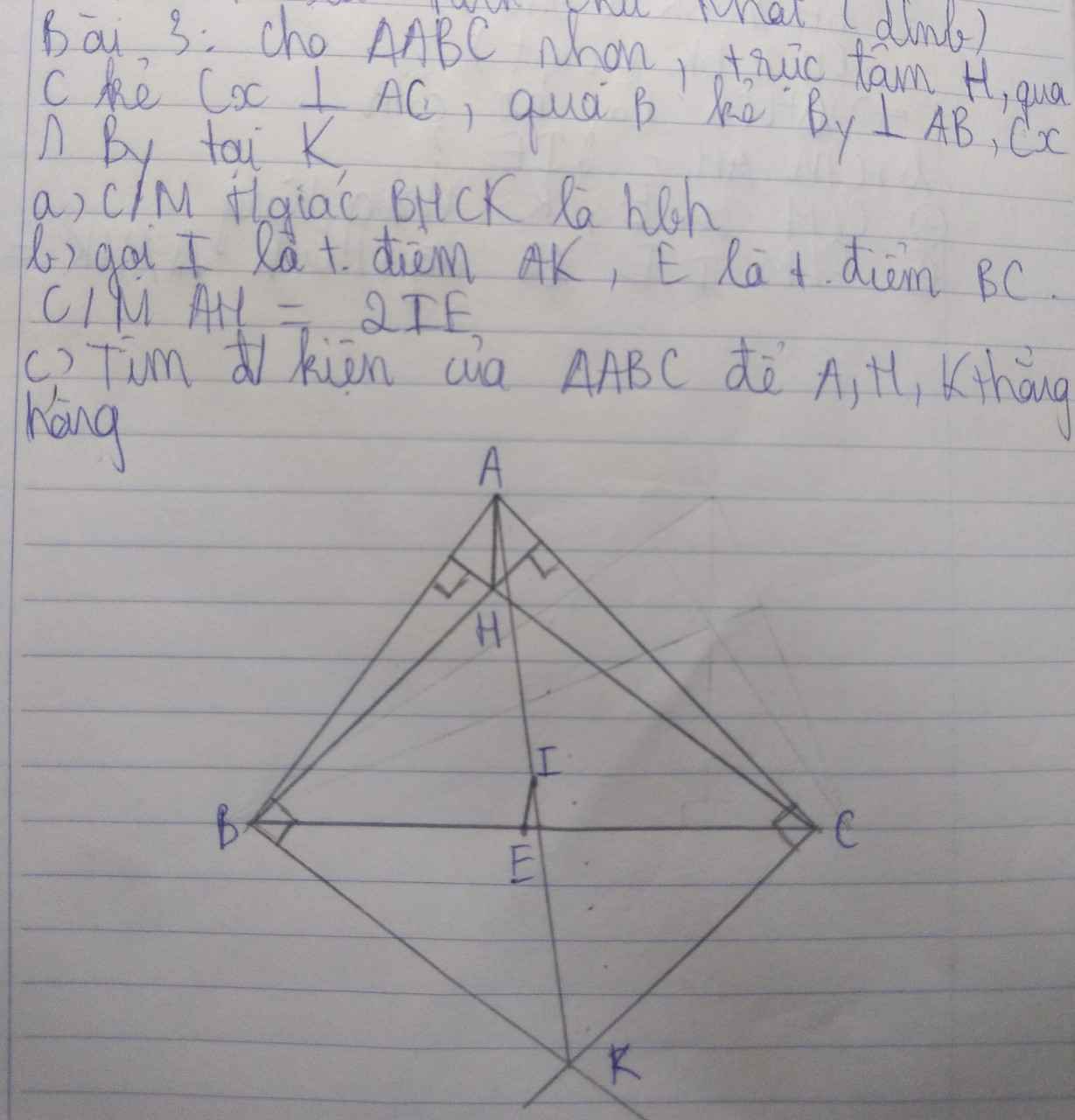



a: \(\overrightarrow{AB}=\left(-3;-2\right)\)
\(\overrightarrow{AC}=\left(1;-4\right)\)
Vì \(\overrightarrow{AB}< >\overrightarrow{AC}\) nên A,B,C ko thẳng hàng
hay A,B,C lập thành 1 tam giác
b: Gọi M là trung điểm của BC
\(\Leftrightarrow\left\{{}\begin{matrix}x_M=\dfrac{2-\left(-2\right)}{2}=2\\y_M=\dfrac{-1-1}{2}=-1\end{matrix}\right.\)
Vậy: M(2;-1)
A(1;3)
\(AM=\sqrt{\left(2-1\right)^2+\left(-1-3\right)^2}=\sqrt{17}\)