ΔABC có độ dài các cạnh là 3cm, 4cm, 5cm. ΔA'B'C' đồng dạng ΔABC và có diện tích là 54cm2. tính các cạnh của ΔA'B'C'.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MN
20 tháng 2 2021
Câu 2. Tam giác nào là tam giác vuông trong các tam giác có độ dài ba cạnh như sau :
A. 3cm; 5cm; 7cm
B. 4cm; 6cm; 8cm
C. 5cm; 7cm; 8cm
D. 3cm; 4cm; 5cm
\(3^2+4^2=5^2\)
Cái này còn được gọi là tam giác Ai Cập nữa nhé :))
HQ
Hà Quang Minh
Giáo viên
20 tháng 9 2023
Theo bất đẳng thức tam giác:
a) Ta xét :
4 + 5 > 7
4 + 7 > 5
5 + 7 > 4
\( \Rightarrow \) Cả 3 cạnh của tam giác đều thỏa mãn bất đẳng thức tam giác
\( \Rightarrow \) a là tam giác
b) Ta xét :
2 + 4 = 6
\( \Rightarrow \) Cả 3 cạnh của tam giác không thỏa mãn bất đẳng thức tam giác
\( \Rightarrow \) b không là tam giác
c) Ta xét :
3 + 4 < 8
\( \Rightarrow \) Cả 3 cạnh của tam giác không thỏa mãn bất đẳng thức tam giác
\( \Rightarrow \) c không là tam giác
CM
29 tháng 9 2018
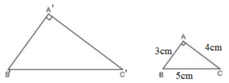
Xét ΔABC có: AB2 + AC2 = 32 + 42 = 25 = 52 = BC2
⇒ ΔABC vuông tại A (Định lý Pytago đảo)
⇒ Diện tích tam giác ABC bằng:
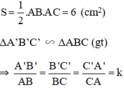
(với k là tỉ số đồng dạng).
Lại có tỉ số diện tích bằng bình phương tỉ số đồng dạng
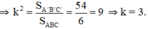
⇒ A’B’ = 3.AB = 3.3 = 9 (cm)
B’C’ = 3.BC = 3.5 = 15 (cm)
C’A’ = 3.CA = 3.4 = 12 (cm)
Vậy độ dài ba cạnh của tam giác lần lượt là 9cm, 12cm, 15cm.
CM
17 tháng 8 2018
a) Hình tròn có bán kính 2cm có diện tích : S = π. 2 2 = 4π ( c m 2 )
b) Hình vuông có độ dài cạnh 3,5cm có diện tích : S = 3 , 5 2 = 12,25 ( c m 2 )
c) tam giác có các cạnh 3cm,4cm,5cm nên nó là tam giác vuông
Khi đó tam giác có diện tích: S =(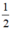
).3.4 =6(
c
m
2
)
d) Nửa mặt cầu bán kính 4cm có diện tích : S= (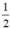
).4.
π
.
4
2
= 32
π
(
c
m
2
)
Vậy trong các hình trên thì nửa mặt cầu bán kính 4cm có diện tích lớn nhất
Vậy chọn đáp án (D)
Lời giải:
Giả sử $AB=3, AC=4, BC=5$ (cm)
Vì $3^2+4^2=5^2$ nên theo định lý Pitago đảo thì $ABC$ là tam giác vuông tại $A$
$A'B'C'$ đồng dạng với $ABC$ nên $A'B'C'$ là tam giác vuông tại $A'$
$\Rightarrow S_{A'B'C'}=\frac{A'B'.A'C'}{2}=54\Rightarrow A'B'.A'C'=108(*)$ (cm)
$ABC\sim A'B'C'\Rightarrow \frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{C'A'}{CA}$
$\Leftrightarrow \frac{A'B'}{3}=\frac{B'C'}{5}=\frac{C'A'}{4}(**)$
Từ $(*); (**)$ suy ra $A'B'=9; B'C'=15; C'A'=12$ (cm)