Theo kế hoạch, một công ty dự định sản xuất một số lượng mũ chắn giọt bắn trong 20 ngày (số mũ chắn giọt bắn sản xuất mỗi ngày là bằng nhau). Thực tế, để tăng cường phòng chống dịch, năng suất sản xuất của công ty tăng 25% nên chỉ trong 17 ngày, công ty hoàn thành số lượng mũ chắn giọt bắn theo kế hoạch và còn sản xuất được thêm 500 chiếc. Hỏi theo kế hoạch, công ty dự định sản xuất bao nhiêu mũ chắn giọt bắn?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số mặt nạ mà đội làm dự kiến trong 1 ngày là x(chiếc, x∈N*)
Thời gian hoàn thành công việc nếu đội tăng năng suất lên 10 chiếc mỗi ngày là : \(\dfrac{720}{x+10}\) (ngày)
Thời gian hoàn thành công việc nếu đội giảm năng suất xuống 20 chiếc mỗi ngày là: \(\dfrac{720}{x-20}\) (ngày)
Theo đề bài ra ta có:
\(\dfrac{720}{x-20}-\dfrac{720}{x+10}=4\)
Giải PT trên ta được x=80
Vậy mỗi ngày đội dự định làm 80 chiếc mặt nạ

2] cao của hình trụ là h (cm)
Đk: h > p
Ta có: Sxq = 2πRh
Stp = 2πRh + 2πR^2
Theo bài ra ta có: Stp = 2Sxq
=> 2πRh + 2πR^2 = 2.2πRh
⇔ 2πR^2 = 2πRh
⇒ h = R = 6 cm
Thể tích V = πR^2.h = π.6^2.6 = 216π (cm3)
Vậy . . .

Gọi số khẩu trang ban đầu tổ phải may là x
=>Lúc sau tổ may được x+150
Theo đề, ta có: \(\dfrac{x}{120}-\dfrac{x+150}{150}=2\)
=>x/120-x/150-1=2
=>x/600=3
=>x=1800

Gọi số sản phẩm tổ dự định làm theo kế hoạch là x (sản phẩm, ![]() ).
).
Thiết lập được PT:
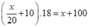
Từ đó tìm được x = 800 (sản phẩm)

Bài 1 :
a, Thay m = 7 vào phương trình trên ta được :
\(x^2-2.8x+49-1=0\)
\(\Leftrightarrow x^2-16x+48=0\)
Ta có : \(\Delta=\left(-16\right)^2-4.48=64\)
\(\Rightarrow x_1=\frac{16-8}{2}=4;x_2=\frac{16+8}{2}=12\)
b, \(x^2-2\left(m+1\right)x+m^2-1=0\)
ta có : \(\Delta=\left[-2\left(m+1\right)\right]^2-4\left(m^2-1\right)=\left(2m+2\right)^2-4m^2+4\)
\(=4m^2+8m-4m^2+4=8m+4\)
Để phương trình có 2 nghiệm thì \(\Delta\ge0\)hay \(8m+4\ge0\Leftrightarrow m\ge-1\)
Theo Vi et ta có : \(\hept{\begin{cases}x_1+x_2=-\frac{b}{a}=2m+2\\x_1x_2=\frac{c}{a}=m^2-1\end{cases}}\)
mà \(x_1+x_2=2m+2\Leftrightarrow\left(x_1+x_2\right)^2=4m^2+8m+4\)
\(\Leftrightarrow x_1^2+x_2^2=4m^2+8m+4-2x_1x_2=4m^2+8m+4-2m^2+2=2m^2+8m+6\)
\(M=2m^2+8m+6-m^2+1=m^2+8m+7\)
\(=m^2+8m+16-9=\left(m+4\right)^2-9\)
Do \(m\ge-1\)nên \(m+4\ge3\)
Suy ra \(M=\left(m+4\right)^2-9\ge9-9=0\)
Vậy GTNN M là 0 khi m = -1

Thực tế tổ sản xuất làm được số sản phẩm mỗi ngày là: 30 + (30 : 100 x 10) = 33 (sản phẩm)
Gọi số ngày dự định hoàn thành xong tất cả sản phẩm là x (ngày, x > 2)
Số ngày thực tế hoàn thành xong tất cả sản phẩm là x - 2 (ngày)
Tổng số sản phẩm dự định làm được là: 30x (sản phẩm)
Tổng số sản phẩm thực tế làm được là: 33(x - 2) (sản phẩm)
Theo bài ra, ta có pt: 33(x - 2) - 30x = 15
<=> 33x - 66 - 30x = 15
<=> 3x = 15 + 66
<=> 3x = 81
<=> x = 27 (thỏa mãn)
Vậy số lượng sản phẩm mà tổ phải làm theo kế hoạch là 27 . 30 = 810 (sản phẩm)
Thực tế tổ sản xuất làm được số sản phẩm mỗi ngày là: 30 + (30 : 100 x 10) = 33 (sản phẩm)
Gọi số ngày dự định hoàn thành xong tất cả sản phẩm là x (ngày, x > 2)
Số ngày thực tế hoàn thành xong tất cả sản phẩm là x - 2 (ngày)
Tổng số sản phẩm dự định làm được là: 30x (sản phẩm)
Tổng số sản phẩm thực tế làm được là: 33(x - 2) (sản phẩm)
Theo bài ra, ta có pt: 33(x - 2) - 30x = 15
<=> 33x - 66 - 30x = 15
<=> 3x = 15 + 66
<=> 3x = 81
<=> x = 27 (thỏa mãn)
Vậy số lượng sản phẩm mà tổ phải làm theo kế hoạch là 27 . 30 = 810 (sản phẩm)
tự làm được r:)))
có chắc bài bạn làm đúng ko vậy để mình chép