Cho d là đường trung trực của AC. Lấy điểm B sao cho A và B ở cùng bên đường thẳng d. BC cắt d tại I. điểm M di động trên d.
- So sánh MA + MB với BC.
- Tìm vị trí M trên d để MA + MB nhỏ nhất
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TT
0
Những câu hỏi liên quan
LN
4 tháng 5 2018
a)Nối M với C. Vì a là trung trực của AC mà M thuộc a nên
MA=MC
Mà tam giác MBC có:
MB+MC>BC (Bđt tam giác)
Suy ra: MB+MA>BC
Vậy MA+MB>BC
b) Mik không biết trình bày làm sau nhưng M là trung điểm của AC thì MA+MB nhỏ nhất
.
10 tháng 1
a: M nằm trên đường trung trực của AC nên MA=MC
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=6^2+8^2=100\)
=>\(BC=\sqrt{100}=10\left(cm\right)\)
TH1: M nằm giữa B và C
=>BM+CM=BC
=>MA+MB=BC=10cm
TH2: B,M,C không thẳng hàng
=>B,M,C tạo thành ΔBMC
Xét ΔMBC có MB+MC>BC
=>MB+MA>10
Do đó; MB+MA>=10
b: Vì \(MB+MA>=10\)
nên \(\left(MB+MA\right)_{min}=10\) khi MB+MC=10
=>MB+MC=BC
=>M nằm giữa B và C
=>M là giao điểm của xy với BC
CM
31 tháng 7 2019
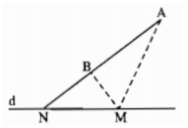
Vì AB không song song với d nên AB cắt d tại N.
Với điểm M bất kỳ thuộc d mà M không trùng với N thì ta có tam giác MAB.
Theo hệ quả bất đẳng thức tam giác ta có:
|MA−MB| < AB
Khi M ≡ N thì
|MA−MB|= AB
Vậy |MA−MB| lớn nhất là bằng AB, khi đó M ≡ N là giao điểm của hai đường thẳng d và AB.