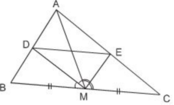
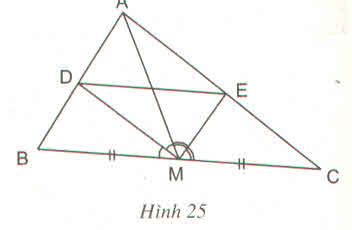
Bài 17 (trang 68 SGK Toán 8 tập 2): Cho tam giác ABC với đường trung tuyến AM. Tia phân giác của góc AMB cắt cạnh AB ở D, tia phân giác của góc AMC cắt cạnh AC ở E. Chứng minh rằng DE // BC (h.25). giúp mik giả vs
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng định lý phân giác cho tam giác ABM:
\(\dfrac{AM}{BM}=\dfrac{AD}{BD}\) (1)
Áp dụng định lý phân giác cho tam giác ACM:
\(\dfrac{AM}{CM}=\dfrac{AE}{CE}\) (2)
Mà AM là trung tuyến \(\Rightarrow BM=CM\) (3)
(1);(2);(3) \(\Rightarrow\dfrac{AD}{BD}=\dfrac{AE}{CE}\Rightarrow\dfrac{AD}{AD+BD}=\dfrac{AE}{AE+CE}\Rightarrow\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
\(\Rightarrow DE||BC\) (định lý talet đảo)

Ta có MD là đường phân giác của tam giác ABM
=> = (1)
ME là đường phân giác của tam giác ACM
=> = (2)
Mà MB = MC( AM là đường trung tuyến)
=> = (3)
từ 1,2,3 => = => DE // BC( Định lí Talet đảo)

a: Xét ΔMAB có MD là phân giác
nên AD/DB=AM/MB=AM/MC
Xét ΔAMC có ME là phân giác
nên AE/EC=AM/MC
=>AD/DB=AE/EC
=>ED//BC
b: Xét ΔABM có DI//BM
nên DI/BM=AI/AM
Xét ΔACM có EI//MC
nên EI/CM=AI/AM
=>DI/BM=EI/CM
=>DI=EI

1: Xét ΔAMB có MD là phân giác
nên AM/MB=AD/DB=AM/MC(1)
Xét ΔAMC có ME là phân giác
nên AM/MC=AE/EC(2)
Từ (1) và (2) suy ra AD/DB=AE/EC
hay DE//BC

1: Xét ΔAMB có MD là phân giác
nên AD/DB=AM/MB=AM/MC(1)
Xét ΔAMC cso ME là phân giác
nên AE/EC=AM/MC(2)
Từ (1)và (2) suy ra AD/DB=AE/EC
hay DE//BC

1: Xet ΔMAB co MD là phân giác
nen AD/DB=AM/MB=AM/MC
Xét ΔMCA có ME là phân giác
nên AE/EC=AM/MC=AD/DB
=>DE//BC
2: Xét ΔABM có DG//BM
nên DG/BM=AG/AM
Xét ΔACM có EG//MC
nên EG/MC=AG/AM
=>DG/BM=EG/MC
mà BM=MC
nên DG=EG
=>G là trung điểm của DE
Để G là trung điểm của AM thì ADME là hình bình hành
=>DM//AC
=>D là trung điểm của AB
=>E là trung điểm của BC
=>AM/MB=AD/DB=1
=>AM=1/2BC
=>góc BAC=90 độ


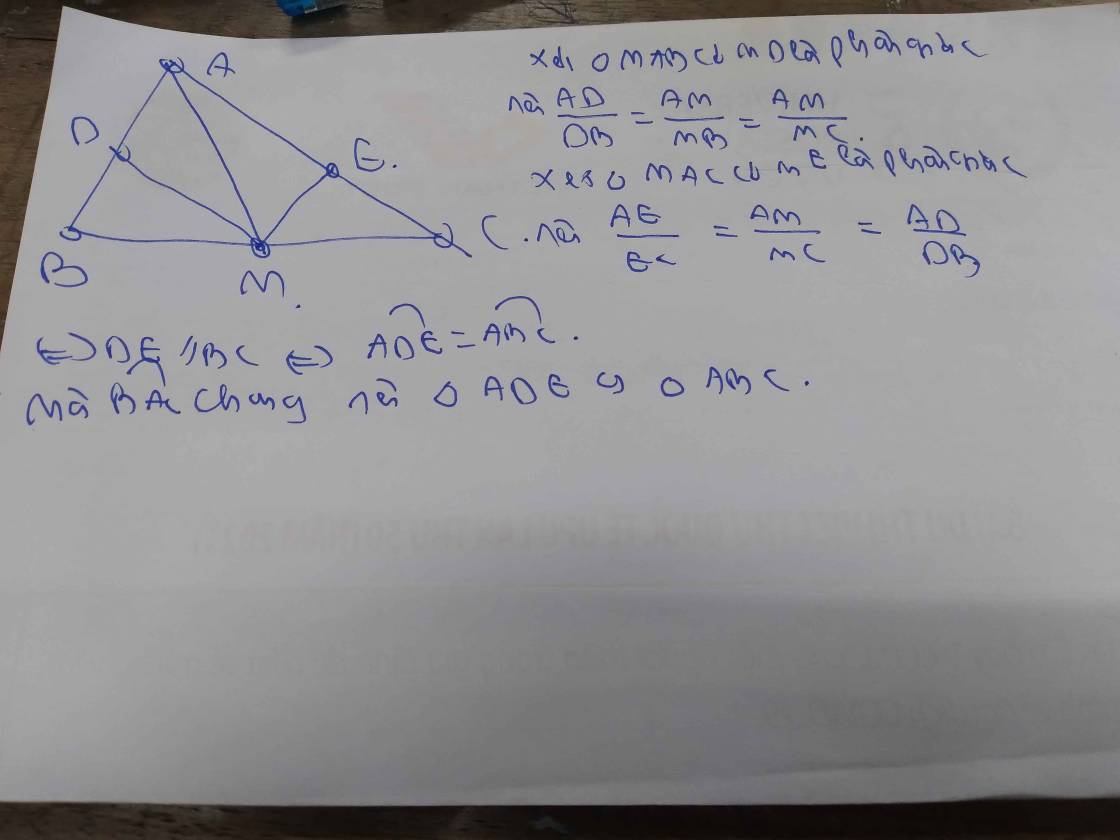
Áp dụng t/c của đường phân giác: Trong tam giác, đường phân giác của 1 góc chia cạnh đối diện thành hai đoạn thẳng tỷ lệ với 2 cạnh kề của 2 đoạn ấy
Xét tg ABM ta có
\(\frac{AD}{AM}=\frac{BD}{BM}\Rightarrow\frac{AD}{BD}=\frac{AM}{BM}\) (1)
Xét tg ACM có
\(\frac{AE}{AM}=\frac{CE}{CM}\Rightarrow\frac{AE}{CE}=\frac{AM}{CM}\) (2)
Mà BM=CM \(\Rightarrow\frac{AM}{BM}=\frac{AM}{CM}\) (3)
Từ (1) (2) (3) \(\Rightarrow\frac{AD}{BD}=\frac{AE}{CE}\) => DE // BC (Talet đảo trong tg)