Tìm điều kiện của tham sô m để hàm số y=(m-1)x+2 là hàm số bậc nhất
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
a: Để (d) là hàm số bậc nhất thì 2m-2<>0
hay m<>1
b: Để (d) là hàm số đồng biến thì 2m-2>0
hay m>1
c: Hàm số (d') đồng biến vì a=4>0
Bài 2:
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}-x+6=3x-6\\y=-x+6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=3\end{matrix}\right.\)

a.
Hàm là hàm số bậc nhất khi:
\(2m-1\ne0\Leftrightarrow m\ne\dfrac{1}{2}\)
b.
Hàm đồng biến trên R khi:
\(2m-1>0\Leftrightarrow m>\dfrac{1}{2}\)
a) Để hàm số là hàm số bậc nhất thì \(2m-1\ne0\)
hay \(m\ne\dfrac{1}{2}\)
b) Để hàm số đồng biến thì 2m-1>0
hay \(m>\dfrac{1}{2}\)

Lời giải:
a. Để hs trên là hàm bậc nhất thì:
$4m2-4m+1\neq 0$
$\Leftrightarrow (2m-1)^2\neq 0$
$\Leftrightarrow 2m-1\neq 0$
$\Leftrightarrow m\neq \frac{1}{2}$
b.
$f(1)=(4m^2-4m+1).1-3=4m^2-4m-2=6$
$\Leftrightarrow 4m^2-4m-8=0$
$\Leftrightarrow m^2-m-2=0$
$\Leftrightarrow (m+1)(m-2)=0$
$\Leftrightarrow m=-1$ hoặc $m=2$


Đáp án A
Hàm số bậc nhất là hàm số có dạng: y = ax + b (a ≠ 0)
Để hàm số đã cho là hàm số bậc nhất thì:
2m - 4 ≠ 0 ⇒ 2m ≠ 4 ⇒ m ≠ 2

Hàm số y=(m-5)+3 (1)
a) Điều kiện của m để hàm số (1) là hàm số bậc nhất
m-5≠0 ➜ m≠5
Vậy m≠5 để hàm số (1) là hàm số bậc nhất.
b) Điều kiện của m để đồ thị của hàm số cắt đồ thị hàm số y=-2x+1
m-5≠-2 ➜ m≠3
Vậy m≠3 để đồ thị của hàm số cắt đồ thị hàm số y=-2x+1.
có gì sai cái nói tui nghen![]()
![]()

\(a,\Leftrightarrow\left\{{}\begin{matrix}2-m>0\\m-4>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m< 2\\m>4\end{matrix}\right.\Leftrightarrow m\in\varnothing\\ b,\Leftrightarrow2-m=m-4\Leftrightarrow m=3\\ c,\Leftrightarrow2-m\ne m-4\Leftrightarrow m\ne3\)

a) Để hàm số \(y = m{x^4} + (m + 1){x^2} + x + 3\) là hàm số bậc hai thì:
\(\left\{ \begin{array}{l}m = 0\\m + 1 \ne 0\end{array} \right.\) tức là \(m = 0.\)
Khi đó \(y = {x^2} + x + 3\)
Vây \(m = 0\) thì hàm số đã cho là hàm số bậc hai \(y = {x^2} + x + 3\)
b) Để hàm số \(y = (m - 2){x^3} + (m - 1){x^2} + 5\) là hàm số bậc hai thì:
\(\left\{ \begin{array}{l}m - 2 = 0\\m - 1 \ne 0\end{array} \right.\) tức là \(m = 2.\)
Khi đó \(y = (2 - 1){x^2} + 5 = {x^2} + 5\)
Vây \(m = 2\) thì hàm số đã cho là hàm số bậc hai \(y = {x^2} + 5\)
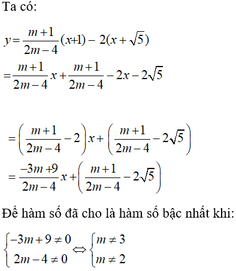
Để đây là hàm số bậc nhất thì m-1<>0
hay m<>1