Đáp án: with

Giải thích: be happy with: vui vẻ với điều gì đó

with

be happy with: vui vẻ, hạnh phúc

315 kh

>

3 tạ15 kg=315kg

4,3 > 4,27 

TXĐ: `D=RR\\{π/2+kπ ; -π/4 +kπ}`

Mà `-π/2+k2π` và `π/2+k2π \in π/2 +kπ`

`=>` Không nằm trong TXĐ.

a/ \(F_{ms}=F_k\Leftrightarrow\mu mg=F_k=0,2.2.10=4\left(N\right)\)

b/ \(F_{ms}=-ma\Leftrightarrow a=-\dfrac{F_{ms}}{m}=-\mu g=-0,2.10=-2\left(m/s^2\right)\)

\(S=v_0t+\dfrac{1}{2}at^2=v_0t-t^2\)

Nếu đề bài ko sai thì v0=0 (m/s) thì thời gian đi hết bằng 0 sẽ nhỏ nhất thôi, bởi vì nhìn cái hàm kia là biết có 3 đại lượng S,v0 và t luôn liên hệ với nhau, thay đổi v0 thì sẽ dẫn đến thay đổi t (nếu coi S là const), nên tui nghĩ chỉ có thể là bằng 0 thôi. Bạn thử lên xem giáo viên nói thế nào đi về cta bàn tiếp

1A

Sau ''where'' là S và căn cứ vào nghĩa của câu nha em

2A 

Trước ''whom'' là chủ ngữ chỉ người và ''girl'' là đối tượng được nghĩ tới

Câu 2 này giải thích vậy không biết em có hiểu không :)))?

\(y'=\dfrac{\left(-2x+2\right)\left(x-3\right)-\left(-x^2+2x+c\right)}{\left(x-3\right)^2}=\dfrac{-x^2+6x-6-c}{\left(x-3\right)^2}\)

\(\Rightarrow\) Cực đại và cực tiểu của hàm là nghiệm của: \(-x^2+6x-6-c=0\) (1)

\(\Delta'=9-\left(6+c\right)>0\Rightarrow c< 3\)

Gọi \(x_1;x_2\) là 2 nghiệm của (1) \(\Rightarrow\left\{{}\begin{matrix}-x_1^2+6x_1-6=c\\-x_2^2+6x_2-6=c\end{matrix}\right.\)

\(\Rightarrow m-M=\dfrac{-x_1^2+2x_1+c}{x_1-3}-\dfrac{-x_2^2+2x_2+c}{x_2-3}=4\)

\(\Leftrightarrow\dfrac{-2x_1^2+8x_1-6}{x_1-3}-\dfrac{-2x_2^2+8x_2-6}{x_2-3}=4\)

\(\Leftrightarrow2\left(1-x_1\right)-2\left(1-x_2\right)=4\)

\(\Leftrightarrow x_2-x_1=2\)

Kết hợp với Viet: \(\left\{{}\begin{matrix}x_2-x_1=2\\x_1+x_2=6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=2\\x_2=4\end{matrix}\right.\)

\(\Rightarrow c=2\)

Có 1 giá trị nguyên

\(=\dfrac{2^{15}\cdot3^8}{3^6\cdot2^6\cdot2^9}+\dfrac{9^3\cdot71}{3^2\cdot71}=3^2+81=90\)

Lời giải:

$\frac{x-2y}{3z}$ có thể nhận giá trị lớn nhất nếu $x$ lớn nhất và $y,z$ nhỏ nhất có thể.

$x$ lớn nhất có thể nhận là $14$ (theo điều kiện)

$y,z$ nhỏ nhất có thể nhận là $1,2$ (do $y,z$ phân biệt)

Nếu $x=14, y=1,z=2$ thì $\frac{x-2y}{3z}=2$

Nếu $x=14; y=2, z=1$ thì $\frac{x-2y}{3z}=\frac{10}{3}>2$

Đáp án D.

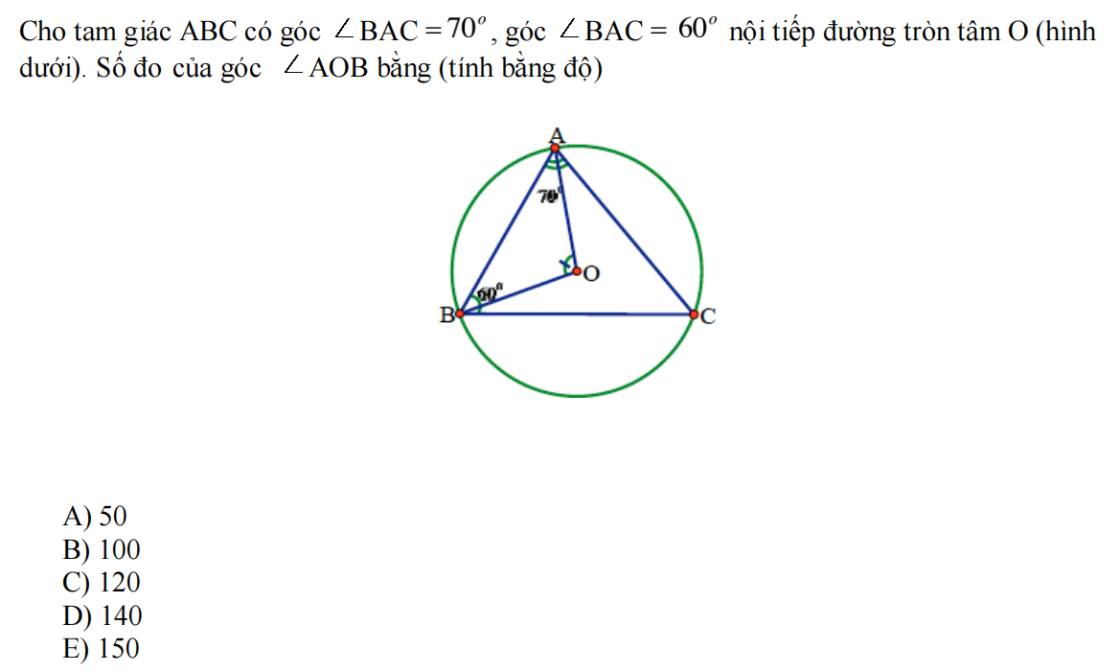
\(\widehat{ACB}=180^0-\left(\widehat{BAC}+\widehat{ABC}\right)=50^0\)

\(\Rightarrow\widehat{AOB}=2.\widehat{ACB}=100^0\) (góc ở tâm gấp đôi góc nội tiếp chắn cùng dây cung)

dạ em cám ơn thầy ạ!