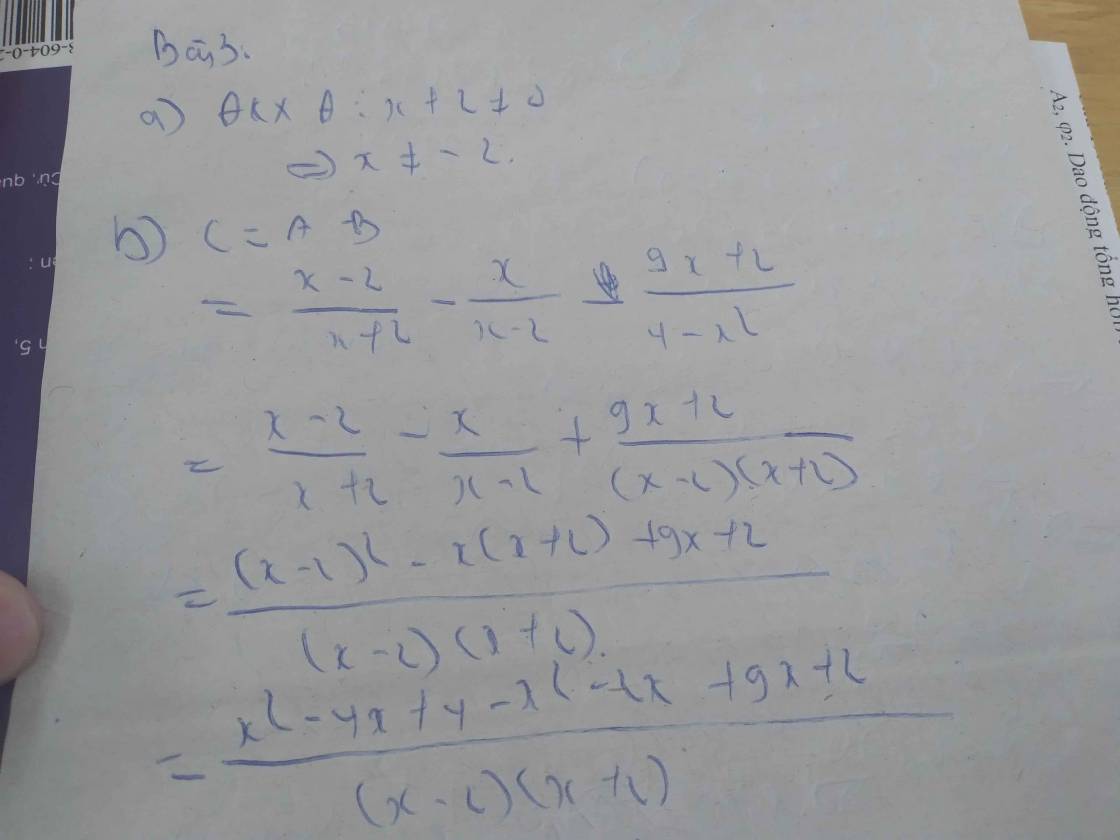Ai giúp mk bài 3 vs ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Câu a:
Số phần trăm chỉ số học sinh của trường viết chữ rõ ràng:
\(\dfrac{5}{8}\). 100 = 62,5 (%)
Số phần trăm chỉ số học sinh của trường viết chữ xấu:
100% - 20% - 62,5% = 17,5%
Tổng số học sinh của trường là:
70 : 17,5% = 400 (hs)
Số học sinh của trường viết chữ đẹp:
400 . 20% = 80 (hs)
Số học sinh của trường viết chữ rõ ràng:
400 - 80 - 70 = 250 (hs)
Câu b:
Tổng số học sinh của trường viết chữ xấu và viết rõ ràng là:
70 + 250 = 320 (hs)
Tỉ số phần trăm học sinh của trường viết chữ xấu và viết chữ rõ ràng so với số học sinh toàn trường là:
320 : 400 . 100% = 80%
Cách 2 của câu b:
Tỉ số phần trăm học sinh của trường viết chữ xấu và viết chữ rõ ràng so với số học sinh toàn trường là:
62,5% + 17,5% = 80%
TƯƠNG TÁC NHA!!![]()


Bài 4:
a: Ta có: \(\widehat{OAB}=\widehat{ODC}\)
\(\widehat{OBA}=\widehat{OCD}\)
mà \(\widehat{ODC}=\widehat{OCD}\)
nên \(\widehat{OAB}=\widehat{OBA}\)
hay ΔOAB cân tại O

x,y là số nguyên => x;y-2 \(\inƯ\left(3\right)=\left\{-3;-1;1;2\right\}\)
Ta có bảng
| x | -3 | -1 | 1 | 3 |
| y-2 | -1 | -3 | 3 | 1 |
| y | 1 | -1 | 5 | 3 |
Vậy (x;y)={(-3;1);(-1;-1);(1;5);(3;3)}

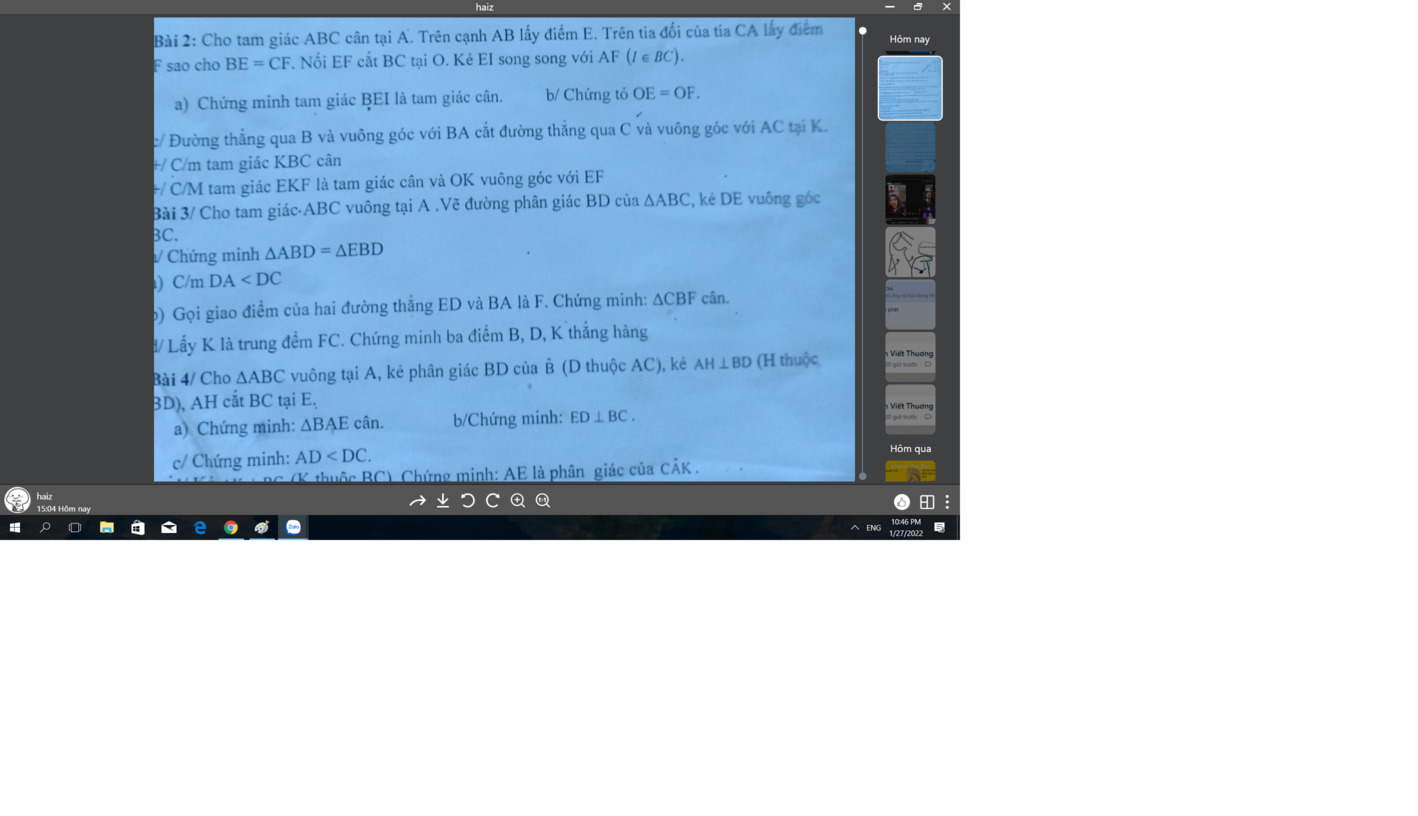
Bài 3:
a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔABD=ΔEBD
b: Ta có: ΔABD=ΔEBD
nên DA=DE
mà DE<DC
nên DA<DC
c: Xét ΔADF vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADF}=\widehat{EDC}\)
Do đó: ΔADF=ΔEDC
Suy ra: AF=EC
Ta có: BA+AF=BF
BE+EC=BC
mà BA=BE
và AF=EC
nên BF=BC
hay ΔBFC cân tại B
d: Ta có: BF=BC
nên B nằm trên đường trung trực của BC(1)
Ta có: DF=DC
nên D nằm trên đường trung trực của BC(2)
Ta có: KF=KC
nên K nằm trên đường trung trực của BC(3)
Từ (1), (2) và (3) suy ra B,D,K thẳng hàng

ĐKXĐ: \(-1\le x\le3\)
Đặt \(\sqrt{x+1}+\sqrt{3-x}=t\ge\sqrt{x+1+3-x}=2\)
\(\Rightarrow4+2\sqrt{-x^2+2x+3}=t^2\)
\(\Rightarrow\sqrt{-x^2+2x+3}=\dfrac{t^2-4}{2}\) (1)
Phương trình trở thành:
\(t-\dfrac{t^2-4}{2}=2\)
\(\Leftrightarrow2t-t^2=0\Rightarrow\left[{}\begin{matrix}t=0\left(loại\right)\\t=2\end{matrix}\right.\)
Thế vào (1):
\(\Rightarrow\sqrt{-x^2+2x+3}=0\)
\(\Rightarrow\left[{}\begin{matrix}x=-1\\x=3\end{matrix}\right.\)