a) Xét ΔHBA và ΔABC có:

^A=^H=90^o

^HAB=^ACB(cùng phụ với ^ABC)

→ ΔHBA∼ΔABC(g.g)

b) Áp dụng định lí Pytago vào tam giác vuông ABC, ta có:

\(BC=\sqrt{20^2+15^2}=25cm\)

\(S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}AB.AC\)

\(\rightarrow AH.BC=AB.AC\)

\(\rightarrow AH=\dfrac{AB.AC}{BC}=12cm\)

c) Xét ΔAHB và ΔCHA có:

^AHB=^CHA=90^o

^HCA=^HAB(cùng phụ với ^ABC)

→ ΔAHB∼ΔCHA(g.g)

\(\rightarrow\dfrac{AH}{HB}=\dfrac{HC}{AH}\left(tươngứng\right)\)

\(\rightarrow AH^2=HB.HC\)

a,xét ΔABC và ΔAHC, có:

góc BAC=góc AHC(=90 độ)

góc C chung

=>ΔABC đồng dạng ΔAHC(g-g)

Bài 2: 

Xét ΔABC có AD là đường phân giác ứng với cạnh BC

nên \(\dfrac{AB}{AC}=\dfrac{BD}{CD}\)

\(\Leftrightarrow\dfrac{AB}{AC}=\dfrac{1}{3}\)

\(\Leftrightarrow\dfrac{BH}{CH}=\dfrac{1}{9}\)

cảm ơn nhiều ạ

Giải giúp mình với ạ 

dùng sin,cos,tan thôi bn

Hình vẽ:

Lời giải:

1.

Xét tam giác $BHA$ và $BAC$ có:

$\widehat{B}$ chung

$\widehat{BHA}=\widehat{BAC}=90^0$

$\Rightarrow \triangle BHA\sim \triangle BAC$ (g.g)

$\Rightarrow \frac{BH}{BA}=\frac{BA}{BC}\Rightarrow BA^2=BH.BC$

Tương tự, ta cũng cm được: $\triangle CHA\sim \triangle CAB$ (g.g)

$\Rightarrow CA^2=CH.CB$

Do đó:

$CA^2+CB^2=BH.BC+CH.CB=BC(BH+CH)=BC.BC=BC^2$ 

(đpcm)

b. Xét tam giác $BHA$ và $AHC$ có:

$\widehat{BHA}=\widehat{AHC}=90^0$

$\widehat{HBA}=\widehat{HAC}$ (cùng phụ $\widehat{BAH}$)

$\Rightarrow \triangle BHA\sim \triangle AHC$ (g.g)

$\Rightarrow \frac{BH}{AH}=\frac{HA}{HC}$

$\Rightarrow AH^2=BH.CH$

c.

$\frac{1}{AB^2}+\frac{1}{AC^2}=\frac{AB^2+AC^2}{AB^2.AC^2}$

$=\frac{BC^2}{AB^2.AC^2}=(\frac{BC}{AB.AC})^2=(\frac{BC}{2S_{ABC}})^2$

$=(\frac{BC}{AH.BC})^2=\frac{1}{AH^2}$

.d. Hiển nhiên theo công thức diện tích. 

Phần c đơn giản lắm :) Vừa nghĩ ra tiếp :

Ta có :

• \(4.\left(S_{ABC}\right)^2=\left(2.S_{ABC}\right)^2\)

\(\Rightarrow\left(AB.AC\right)^2=\left(AH.BC\right)^2\)

\(\Rightarrow AB^2.AC^2=AH^2.BC^2\)

Mà \(BC^2=AB^2+AC^2\)( Pythagores )

\(\Rightarrow AB^2.AC^2=AH^2\left(AB^2+AC^2\right)\)

\(\Rightarrow\frac{1}{AH^2}=\frac{AB^2+BC^2}{AB^2.AC^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\)

Vậy...

Ngồi nháp rồi nghĩ ra phần a  :) Sẽ cập nhật khi nghĩ được b , c

[ Tự vẽ hình ]

Áp dụng định lý Pythagores có :

• \(AB^2+AC^2=BC^2\)
• \(AH^2=AC^2-HC^2=AB^2-BH^2\)

\(\Rightarrow AH^2=\frac{AC^2-HC^2+AB^2-HB^2}{2}\)

\(=\frac{\left(AB^2+AC^2\right)-\left(HB^2+HC^2+2HB.HC\right)+2HB.HC}{2}\)

\(=\frac{BC^2-\left(HB+HC\right)^2+2HB.HC}{2}\)

\(=\frac{BC^2-BC^2+2HB.HC}{2}\)

\(=\frac{2HB.HC}{2}\)

\(=HB.HC\)

Vậy \(AH^2=HB.HC.\)

Ta có:

\(sinC=\dfrac{AB}{BC}\Rightarrow sin30^o=\dfrac{AB}{5}\)

\(\Rightarrow AB=5\cdot sin30^o=\dfrac{5}{2}\left(cm\right)\) 

Mà: \(tanC=\dfrac{AB}{AC}\Rightarrow tan30^o=\dfrac{\dfrac{5}{2}}{AC}\)

\(\Rightarrow AC=\dfrac{\dfrac{5}{2}}{tan30^o}=\dfrac{5\sqrt{3}}{2}\left(cm\right)\) 

Theo hệ thức đường cao cạnh góc vuông và cạnh huyền ta có:

\(AB\cdot AC=AH\cdot BC\)

\(\Rightarrow AH=\dfrac{AB\cdot AC}{BC}=\dfrac{\dfrac{5}{2}\cdot\dfrac{5\sqrt{3}}{2}}{5}=\dfrac{5\sqrt{3}}{4}\left(cm\right)\)

Ta có: \(\left\{{}\begin{matrix}HB=\dfrac{AB^2}{BC}=\dfrac{\left(\dfrac{5}{2}\right)^2}{5}=\dfrac{5}{4}\left(cm\right)\\HC=\dfrac{AC^2}{BC}=\dfrac{\left(\dfrac{5\sqrt{3}}{2}\right)^2}{5}=\dfrac{15}{4}\left(cm\right)\end{matrix}\right.\)   

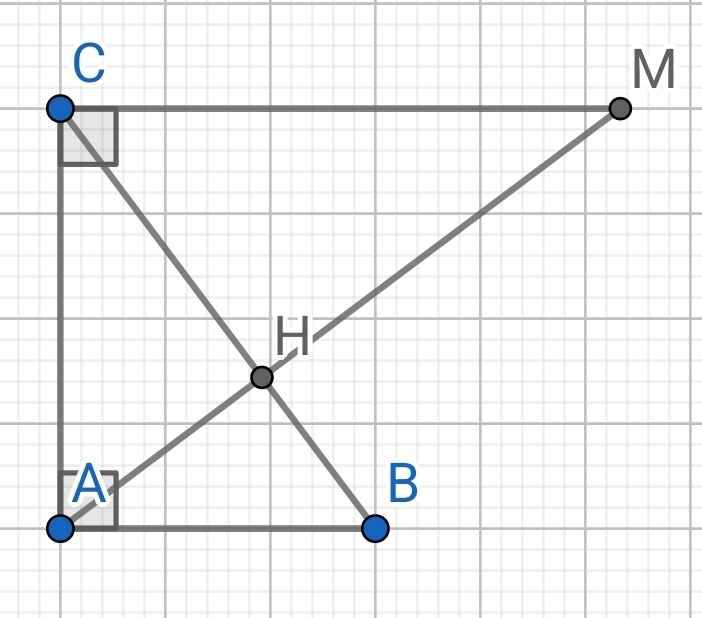 a) ∠ABC = 90⁰ - 30⁰ = 60⁰

sinC = AB/BC

⇒ AB = BC.sinC

= 5.sin30⁰

= 5.1/2

= 5/2 (cm)

sinB = AC/BC

⇒ AC = BC.sinB

= 5.sin60⁰

= 5√3/2 (cm)

Ta có:

AH.BC = AB.AC

⇒ AH = AB.AC : BC

= 5/2 . 5√3/2 : 5

= 5√3/4 (cm)

AB² = BH.BC

⇒ BH = AB² : BC

= (5/2)² : 5

= 5/4 (cm)

⇒ CH = BC - BH

= 5 - 5/4

= 15/4 (cm)

b) Do AH ⊥ BC (gt)

⇒ CH ⊥ AM

∆ACM vuông tại C có CH là đường cao

⇒ AC² = AH . AM (1)

∆ABC vuông tại A có AH là đường cao

⇒ AC² = CH . CB (2)

Từ (1) và (2) ⇒ AH.AM = CH.CB

a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có

góc B chung

Do đó: ΔABC\(\sim\)ΔHBA

b: ta có: ΔABC\(\sim\)ΔHBA

nên BA/BH=BC/BA

hay \(BA^2=BH\cdot BC\)

a.Xét tam giác ABC và tam giác HBA, có:

^B: chung

^BAC = ^BHA = 90 độ

Vậy tam giác ABC đồng dạng tam giác HBA (g.g)

b.\(\rightarrow\dfrac{AB}{HB}=\dfrac{BC}{AB}\)

\(\Leftrightarrow AB^2=BH.BC\left(đfcm\right)\) (1)

c.Áp dụng định lý pitago \(\Rightarrow BC=\sqrt{6^2+10^2}=2\sqrt{34}\left(cm\right)\)

(1) \(\Leftrightarrow6^2=2\sqrt{34}BH\)

\(\Leftrightarrow BH=\dfrac{9\sqrt{34}}{17}\left(cm\right)\)

Áp dụng định lý pitago trong tam giác ABH \(\Rightarrow AH=\sqrt{6^2-\left(\dfrac{9\sqrt{34}}{17}\right)^2}=\dfrac{15\sqrt{34}}{17}\left(cm\right)\)