Bài 5: Cho tam giác ABC, trung tuyến AM. Từ M kẻ đường thẳng song song với AB cắt AC tại N. Biết AN=MN; BN cắt AM ở O. Chứng minh:
a) Tam giác ABC cân ở A
b) O là trọng tâm của tam giác ABC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
H9
HT.Phong (9A5)
CTVHS
16 tháng 1
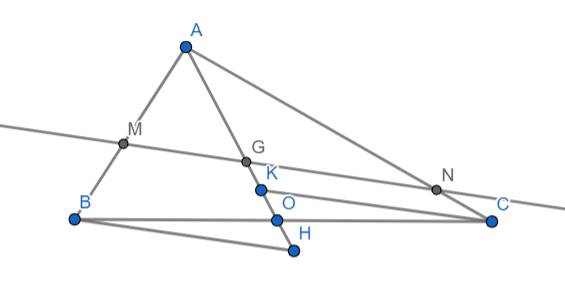
Xét 2 tam giác AMG và ABH ta có:
\(\widehat{BAH}\) chung
\(\widehat{AMG}=\widehat{ABH}\) (cặp góc đồng vị do BH//MG)
\(\Rightarrow\Delta AMG\sim\Delta ABH\left(g.g\right)\)
\(\Rightarrow\dfrac{AB}{AM}=\dfrac{AH}{AG}\) (1)
Xét 2 tam giác ANG và ACK có:
\(\widehat{CAK}\) chung
\(\widehat{ANG}=\widehat{ACK}\) (cặp góc đồng vị do CK//GN)
\(\Rightarrow\Delta ANG\sim\Delta ACK\left(g.g\right)\)
\(\Rightarrow\dfrac{AC}{AN}=\dfrac{AK}{AG}\) (2)
Xét hai tam giác BOH và COK ta có:
\(\widehat{BOH}=\widehat{COK}\) (đối đỉnh)
\(BO=CO\) (AO là đường trung tuyến nên O là trung điểm của BC)
\(\widehat{HBO}=\widehat{KCO}\) (so le trong vì BH//MN và CK//MN ⇒ BH//CK)
\(\Rightarrow\Delta BOH=\Delta COK\left(g.c.g\right)\)
\(\Rightarrow HO=OK\) (hai cạnh t.ứng)
\(\Rightarrow HK=2HO\)
Ta lấy (1) + (2) \(\Rightarrow\dfrac{AB}{AM}+\dfrac{AC}{AN}=\dfrac{AH+AK}{AG}=\dfrac{AH+AH+HK}{AG}=\dfrac{2AH+HK}{AG}\)
\(=\dfrac{2AH+2HO}{AG}=\dfrac{2\left(AH+HO\right)}{AG}=\dfrac{2AO}{AG}\)
Mà G là trọng tâm của tam giác ABC \(\Rightarrow AO=\dfrac{3}{2}AG\)
\(\Rightarrow\dfrac{AB}{AM}+\dfrac{AC}{AN}=\dfrac{2\cdot\dfrac{3}{2}AG}{AG}=2\cdot\dfrac{3}{2}=3\left(đpcm\right)\)
PP
22 tháng 7 2017
<br class="Apple-interchange-newline"><div id="inner-editor"></div>ΔABC, có: M là trung điểm BC và MN //BC
=> MN là đường trung bình ΔABC
=> N là trung điểm NC
=> AN=NC mà AN=MN (gt) => MN=NC
Xét ΔMNC, có : MN=NC
=> ΔMNC cân tại N
=> góc M= góc C (1)
Vì MN//AB
=> góc B= góc M( 2 góc đồng vị) (2)
Từ (1) và (2) => góc B= góc C
Xét ΔABC, có : góc B= góc C
=>
<br class="Apple-interchange-newline"><div id="inner-editor"></div>ΔABC, có: M là trung điểm BC và MN //BC
=> MN là đường trung bình ΔABC
=> N là trung điểm NC
=> AN=NC mà AN=MN (gt) => MN=NC
Xét ΔMNC, có : MN=NC
=> ΔMNC cân tại N
=> góc M= góc C (1)
Vì MN//AB
=> góc B= góc M( 2 góc đồng vị) (2)
Từ (1) và (2) => góc B= góc C
Xét ΔABC, có : góc B= góc C
=> ΔABC cân tại A
30 tháng 6 2022
1: Xét ΔAMC có
MN là đường trung tuyến
MN=AC/2
Do đó:ΔAMC vuông tại M
Xét ΔABC có
AM là đường cao
AM là đường trung tuyến
Do đo: ΔABC cân tại A
2: Xét ΔABC có
BN là đường trung tuyến
AM là đường trung tuyến
BN cắt AM tại O
Do đó: O là trọng tâm của ΔABC
14 tháng 12 2021
Cm: a) Ta có: BA ⊥⊥AC (gt)
HD // AB (gt)
=> HD ⊥⊥AC => ˆHDA=900HDA^=900
Ta lại có: AC ⊥⊥AB (gt)
HE // AC (gt)
=> HE ⊥⊥AB => ˆHEA=900HEA^=900
Xét tứ giác AEHD có: ˆA=ˆAEH=ˆHDA=900A^=AEH^=HDA^=900
=> AEHD là HCN => AH = DE
b) Gọi O là giao điểm của AH và DE
Ta có: AEHD là HCN => OE = OH = OD = OA
=> t/giác OAD cân tại O => ˆOAD=ˆODAOAD^=ODA^ (1)
Xét t/giác ABC vuông tại A có AM là đường trung tuyến
-> AM = BM = MC = 1/2 BC
=> t/giác AMC cân tại M => ˆMAC=ˆCMAC^=C^
Ta có: ˆB+ˆC=900B^+C^=900 (phụ nhau)
ˆC+ˆHAC=900C^+HAC^=900 (phụ nhau)
=> ˆB=ˆHACB^=HAC^ hay ˆB=ˆOADB^=OAD^ (2)
Từ (1) và (2) => ˆODA=ˆBODA^=B^
Gọi I là giao điểm của MA và ED
Xét t/giác IAD có: ˆIAD+ˆIDA+ˆAID=1800IAD^+IDA^+AID^=1800 (tổng 3 góc của 1 t/giác)
=> ˆAID=1800−(IAD+ˆIDA)AID^=1800−(IAD+IDA^)
hay ˆAID=1800−(ˆB+ˆC)=1800−900=900AID^=1800−(B^+C^)=1800−900=900
=> AM⊥DEAM⊥DE(Đpcm)
c) (thiếu đề)
a,Xét ΔΔAMN có : AN=NM
⇒⇒góc NAM =góc NMA
mà góc NMA= góc MAB (vì MN song song với AB)
nên góc NAM =góc MAB hay MA là tia phân giác góc BAC
Xét ΔΔABC ta có:
AM là tia phân giác góc BAC và cũng là đường trung tuyến ứng với cạnh BC
⇒⇒ΔΔABC cân tại A
b, Theo câu a ta có :ΔΔABC cân tại A
⇒⇒góc ABC = góc NCM
Mà góc NMC = góc ABC
NÊN góc NMC= góc NCM
⇒⇒ ΔΔNMC cân tại N
⇒⇒MN=NC
mà NM=AN
Nên AN=NC hay BN là đường trung tuyến ứng với cạnh AC
Ta có: AM là đường trung tuyến ứng với cạnh BC
BN là đường trung tuyến ứng với cạnh AC
mà BN cắt AM tại O
Nên O là trọng tâm của tam giác ABC
a,Xét ΔΔAMN có : AN=NM
⇒⇒góc NAM =góc NMA
mà góc NMA= góc MAB (vì MN song song với AB)
nên góc NAM =góc MAB hay MA là tia phân giác góc BAC
Xét ΔΔABC ta có:
AM là tia phân giác góc BAC và cũng là đường trung tuyến ứng với cạnh BC
⇒⇒ΔΔABC cân tại A
b, Theo câu a ta có :ΔΔABC cân tại A
⇒⇒góc ABC = góc NCM
Mà góc NMC = góc ABC
NÊN góc NMC= góc NCM
⇒⇒ ΔΔNMC cân tại N
⇒⇒MN=NC
mà NM=AN
Nên AN=NC hay BN là đường trung tuyến ứng với cạnh AC
Ta có: AM là đường trung tuyến ứng với cạnh BC
BN là đường trung tuyến ứng với cạnh AC
mà BN cắt AM tại O
Nên O là trọng tâm của tam giác ABC